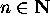 of the equation
of the equation
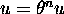 , where
, where 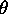 is an ``isomorphism of codes.'' Note (
is an ``isomorphism of codes.'' Note ( )
by Mr. Yves Lecerf, presented by Mr. André Lichnerowicz.
)
by Mr. Yves Lecerf, presented by Mr. André Lichnerowicz.


Weekly Proceedings of the Academy of Science, 257:2597--2600, Meeting of October 28, 1963.
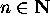 of the equation
of the equation
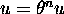 , where
, where 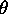 is an ``isomorphism of codes.'' Note (
is an ``isomorphism of codes.'' Note ( )
by Mr. Yves Lecerf, presented by Mr. André Lichnerowicz.
)
by Mr. Yves Lecerf, presented by Mr. André Lichnerowicz.
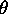 .'' Their properties make it possible to prove that the
equation in
.'' Their properties make it possible to prove that the
equation in 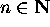 ,
, 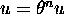 is recursively unsolvable. A
second note will apply this to the demonstration of a conjecture of
Schützenberger relating the Post correspondence problem to the problem of
diagonalization of homomorphisms of free monoids.
is recursively unsolvable. A
second note will apply this to the demonstration of a conjecture of
Schützenberger relating the Post correspondence problem to the problem of
diagonalization of homomorphisms of free monoids.
1. ISOMORPHISMS OF CODES, EPIMORPHISMS OF CODES. ---
a. A conjecture of Schützenberger. --- Given two
nontrivial free monoids 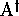 and
and 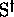 , and given two
homomorphisms
, and given two
homomorphisms 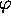 and
and 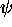 of
of 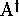 into
into 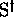 ,
consider the problem of the search for nontrivial solutions
,
consider the problem of the search for nontrivial solutions 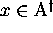 for the equation of diagonalization
for the equation of diagonalization 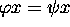 . A result
of Post (
. A result
of Post ( ) is that this equation is recursively unsolvable in the case
of
) is that this equation is recursively unsolvable in the case
of 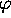 and
and 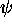 being arbitrary homomorphisms. It is also so when
one restricts
being arbitrary homomorphisms. It is also so when
one restricts 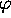 to be a monomorphism; indeed, Chomsky and
Schützenberger remarked (
to be a monomorphism; indeed, Chomsky and
Schützenberger remarked ( ) that this case can be reduced to Post's
Tag-problem (
) that this case can be reduced to Post's
Tag-problem ( ), itself recursively unsolvable according to a result of
Minsky (
), itself recursively unsolvable according to a result of
Minsky ( ). Schützenberger conjectured that the equation
). Schützenberger conjectured that the equation 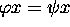 remains still recursively unsolvable when
remains still recursively unsolvable when 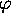 and
and 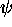 are both monomorphisms.
are both monomorphisms.
b. Isomorphisms of codes. --- Instead of 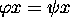 , it is
equivalent to consider the equation
, it is
equivalent to consider the equation 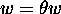 , where
, where
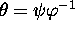 (this is shorthand notation for saying that
(this is shorthand notation for saying that
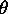 is a bijection of
is a bijection of 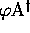 into
into 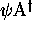 defined by
defined by 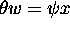 for
for 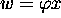 ). For convenience, we will
call the applications such as
). For convenience, we will
call the applications such as 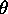 ``isomorphisms of codes.'' The term
recalls that
``isomorphisms of codes.'' The term
recalls that 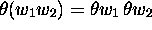 ; and also that,
; and also that, 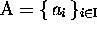 designating the alphabet (generators) of
designating the alphabet (generators) of
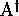 ,
, 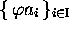 and
and 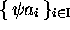 are called ``codes'' on
are called ``codes'' on 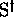 , because, for
an arbitrary y in
, because, for
an arbitrary y in 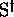 , there exists a set of indices
, there exists a set of indices
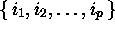 such that
such that 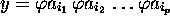 , and the same for
, and the same for 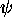 . In fact, it is
especially the study of isomorphisms of codes to which will be devoted the
present Note and the following one.
. In fact, it is
especially the study of isomorphisms of codes to which will be devoted the
present Note and the following one.
c. Definitions of particular ``isomorphisms of codes'' using
relation elements. --- With 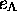 and
and 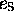 designating the
identity elements respectively of
designating the
identity elements respectively of 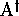 and
and 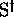 , it
goes without saying implicitly for every
, it
goes without saying implicitly for every 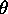 that one has
that one has 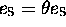 , with
, with 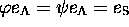 (whenceforth a trivial solution for
(whenceforth a trivial solution for 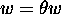 and for
and for 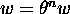 ,
with
,
with 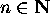 ). This being the case, each particular isomorphism of
codes could be defined by a set of relation elements of the type
). This being the case, each particular isomorphism of
codes could be defined by a set of relation elements of the type
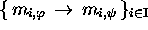 , provided
that
, provided
that 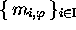 and
and
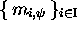 are ``codes'' and that the
correspondence is bijective. Indeed,
are ``codes'' and that the
correspondence is bijective. Indeed, 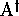 is implicitly defined
by
is implicitly defined
by 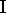 , and
, and 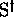 by the symbols used to note the
by the symbols used to note the
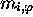 and
and 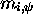 ; and one can interpret the relations like
correspondences
; and one can interpret the relations like
correspondences 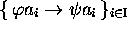 .
.
d. Checking whether a given set of words is a code. --- Further,
the following property will be often called upon: If C and 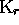 designate respectively a code and a right prefix-code on
designate respectively a code and a right prefix-code on 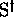 ,
and if
,
and if 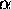 is a symbol (generator of
is a symbol (generator of 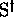 ) not appearing in C
nor in
) not appearing in C
nor in 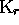 , then, the set
, then, the set 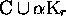 is a code.
In the same way, replacing
is a code.
In the same way, replacing 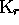 by a left prefix-code
by a left prefix-code 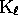 , the set
, the set 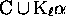 is a code. Let us recall
that any right prefix-code
is a code. Let us recall
that any right prefix-code 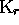 is by definition (
is by definition ( ) such that,
if
) such that,
if 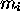 ,
, 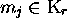 and if, with
and if, with 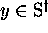 , one has
, one has
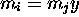 , then
, then 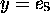 (while for the left prefix-codes, it is
(while for the left prefix-codes, it is
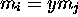 which imposes
which imposes 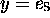 ).
).
e. Epimorphisms of codes. --- One speaks about ``epimorphisms of
codes'' 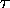 in the case of relations
in the case of relations 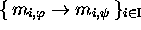 , where
, where 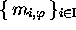 is a complete code
is a complete code 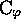 , but where
, but where
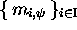 is only constrained not to contain words
other than those of a code
is only constrained not to contain words
other than those of a code 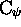 .
REVERSIBLE TURING MACHINES. --- Let MT be a Turing machine of
which
.
REVERSIBLE TURING MACHINES. --- Let MT be a Turing machine of
which 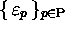 and
and 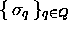 are the sets of states and symbols, and
are the sets of states and symbols, and 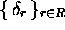 are
tape displacements, which can be
are
tape displacements, which can be 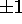 or 0. One can define MT by a set
of quintuples
or 0. One can define MT by a set
of quintuples
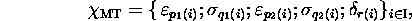
where the indices 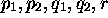 are functions of index i. With
each of the quintuples, let us decide to associate an ``inverse image
quintuple'' (
are functions of index i. With
each of the quintuples, let us decide to associate an ``inverse image
quintuple'' (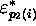 ;
; 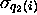 ;
;
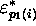 ;
; 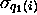 ;
; 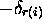 ). The set of
those will generally not constitute a Turing machine; but when it does, we
will say that MT is ``reversible,'' and call the new machine the inverse
image
). The set of
those will generally not constitute a Turing machine; but when it does, we
will say that MT is ``reversible,'' and call the new machine the inverse
image 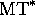 of MT. The
of MT. The 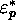 will be known as the
images of
will be known as the
images of 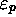 . The substituion of
. The substituion of 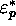 for
for
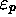 in an instantaneous configuration
in an instantaneous configuration 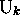 will be known
as transformation of
will be known
as transformation of 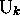 to its image configuration
to its image configuration 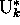 .
The continuations of configurations of
.
The continuations of configurations of 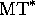 are images of those of
MT, but
are images of those of
MT, but 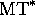 traverses them in the opposite order. Now let us
consider the machine R(MT), whose set of quintuples is
traverses them in the opposite order. Now let us
consider the machine R(MT), whose set of quintuples is
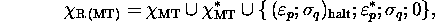
where
Proof. --- It is shown how to proceed from
b. THEOREM 1. --- The halting problem for a
general reversible Turing machine is undecidable. Similarly for the
problem of returning to the initial configuration, and that of the passage
through a given configuration other than the initial configuration.
c. THEOREM 2. --- The equation
(
(
(
(
(
(
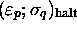 designates any state-symbol
pair for which MT halts. If one starts MT and R(MT) from the same
instantaneous configuration
designates any state-symbol
pair for which MT halts. If one starts MT and R(MT) from the same
instantaneous configuration 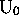 , they pass through the same
configurations as long as MT does not halt (thus possibly indefinitely).
When MT halts, R(MT) continues, traversing in the opposite order the
image configurations of the traversed configurations, and passes by the
image of the initial configuration. R(MT) will be known as the coupling
of MT with its reverse image.
REPRESENTATION OF TURING MACHINES BY EPIMORPHISMS (OR
ISOMORPHISMES) OF CODES. --- Let us be given an arbitrary MT. With each
quintuple having movement +1, that is to say for example
, they pass through the same
configurations as long as MT does not halt (thus possibly indefinitely).
When MT halts, R(MT) continues, traversing in the opposite order the
image configurations of the traversed configurations, and passes by the
image of the initial configuration. R(MT) will be known as the coupling
of MT with its reverse image.
REPRESENTATION OF TURING MACHINES BY EPIMORPHISMS (OR
ISOMORPHISMES) OF CODES. --- Let us be given an arbitrary MT. With each
quintuple having movement +1, that is to say for example
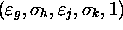 , we associate three
relation elements, namely:
, we associate three
relation elements, namely:
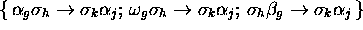 .
With
.
With 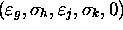 , we associate:
, we associate:
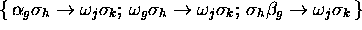 .
With
.
With 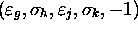 , we associate
, we associate
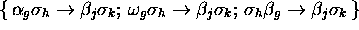 .
Finally, with any symbol
.
Finally, with any symbol 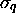 of MT, we associate
of MT, we associate
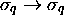 . One can check, by the process given in
paragraph 1d, that the set of these relations defines an
epimorphism of codes. With
. One can check, by the process given in
paragraph 1d, that the set of these relations defines an
epimorphism of codes. With 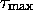 being this set,
being this set, 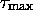 is a representation of MT, because it defines its alphabet and
quintuples. We can, in addition, find, for the instantaneous
configurations of MT, notations such that for any pair of successive
configurations
is a representation of MT, because it defines its alphabet and
quintuples. We can, in addition, find, for the instantaneous
configurations of MT, notations such that for any pair of successive
configurations 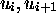 we have
we have 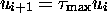 . For
that, a configuration will be composed of a succession of symbols
. For
that, a configuration will be composed of a succession of symbols 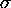 (the string on the tape) into which one will intercalate one of the letters
(the string on the tape) into which one will intercalate one of the letters
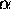 ,
, 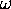 or
or 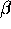 , with an index p equal to that of the state
, with an index p equal to that of the state
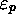 of the machine, and indicating, not only the position
of the machine, and indicating, not only the position
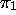 of the next symbol to read, but also the position
of the next symbol to read, but also the position 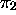 of the
symbol previously written (with a particular convention for the initial
configuration). An
of the
symbol previously written (with a particular convention for the initial
configuration). An 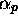 signifies that
signifies that 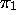 is the first symbol
to its right,
is the first symbol
to its right, 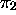 the first on its left. A
the first on its left. A 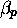 , vice-versa. An
, vice-versa. An
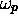 means that
means that 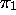 and
and 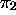 are both the first symbol to the
right of the
are both the first symbol to the
right of the 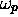 . We have then achieved that
. We have then achieved that
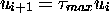 . So certain states
. So certain states 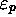 can appear
under only two or one of the forms
can appear
under only two or one of the forms 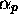 ,
, 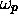 ,
, 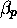 , and
, and
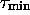 is obtained by removing from
is obtained by removing from 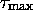 all the
relation elements containing the forms which never appear, so
all the
relation elements containing the forms which never appear, so 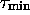 is still such that
is still such that 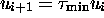 . If
. If 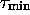 is an isomorphism of codes, MT is reversible.
SIMULATION OF ARBITRARY MT ON REVERSIBLE
is an isomorphism of codes, MT is reversible.
SIMULATION OF ARBITRARY MT ON REVERSIBLE 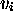 )
on a reversible Turing machine
)
on a reversible Turing machine 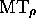 (with configurations
(with configurations
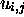 ) so that: (1) when MT passes from
) so that: (1) when MT passes from 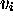 to
to 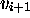 ,
, 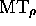 passes from
passes from 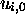 to
to 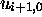 via the intermediary of a
finite number of configurations
via the intermediary of a
finite number of configurations 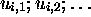 ; (2) we pass
from one
; (2) we pass
from one 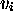 to the next via an epimorphism of codes
to the next via an epimorphism of codes 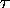 , and from one
, and from one
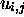 to the next via an isomorphism of codes
to the next via an isomorphism of codes 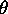 ; (3) if the
initial configurations are
; (3) if the
initial configurations are 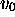 for MT and
for MT and 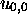 for
for 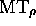 ,
with
,
with 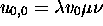 , then for any i, one has
, then for any i, one has 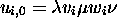 , where
, where 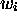 is a string, and where
is a string, and where 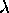 ,
, 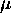 ,
,
 are three symbols which appear neither in
are three symbols which appear neither in 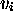 nor in
nor in 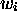 , so that
knowing
, so that
knowing 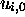 gives
gives 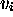 and
and 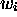 ; (4) there are symbols
; (4) there are symbols 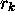 of
which each one represents a relation element of
of
which each one represents a relation element of 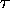 other than that of
identity; a blank symbol b; and for any i we have
other than that of
identity; a blank symbol b; and for any i we have
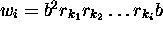 , where
, where 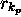 is the relation
invoked by
is the relation
invoked by 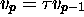 . Thus,
. Thus, 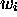 represents the history of the
computation of MT until time i; (5)
represents the history of the
computation of MT until time i; (5) 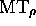 halts on the
halts on the
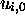 corresponding to the halting of MT, and them only; (6) the
machine
corresponding to the halting of MT, and them only; (6) the
machine 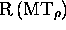 , coupling
, coupling 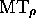 with its
reverse image, starting from
with its
reverse image, starting from 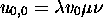 passes through the
image configuration
passes through the
image configuration 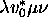 if and only if MT, starting from
if and only if MT, starting from
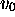 , halts; (7) there exists for R(
, halts; (7) there exists for R(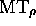 ) certain
instantaneous configurations
) certain
instantaneous configurations 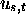 such that, when started at
such that, when started at 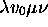 , R(
, R(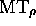 ) cannot reach those configurations other
than by passing through
) cannot reach those configurations other
than by passing through 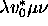 (i.e., if MT,
starting from
(i.e., if MT,
starting from 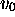 , halts). One can thus arrange that the return of of
R(
, halts). One can thus arrange that the return of of
R(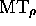 ) to
) to 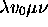 (or the passage through
(or the passage through
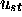 framed by
framed by 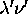 instead of
instead of 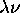 ) is conditional
on the halting of MT.
) is conditional
on the halting of MT.
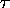 , presumed to be
given by a set of relation elements
, presumed to be
given by a set of relation elements 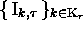 to the set of relation elements
to the set of relation elements  defining
defining 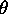 and
and 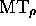 . We delimit the principles of this construction, by showing how
to simulate an
. We delimit the principles of this construction, by showing how
to simulate an 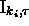 of the form
of the form
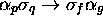 . With this, we associate: an
instruction
. With this, we associate: an
instruction
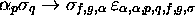 ,
where the symbol
,
where the symbol 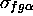 marks the place where one must modify
marks the place where one must modify
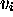 , and the nature of the modification; instructions allowing control to
be lead to the left from
, and the nature of the modification; instructions allowing control to
be lead to the left from  through a state
through a state 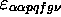 ; an instruction
; an instruction 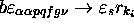 , where
, where 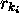 represents
represents
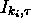 , supplementing
, supplementing 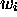 ; working instructions moving
; working instructions moving  and
possibly also
and
possibly also 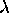 ,
, 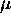 and the entire
and the entire 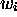 , to restore the
necessary blanks in
, to restore the
necessary blanks in 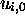 and then defer control in
and then defer control in
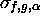 with a state
with a state 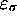 ; an instruction
; an instruction
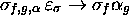 which
supplements
which
supplements 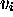 in
in 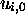 .
.
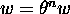 , where
, where 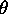 is an isomorphism of codes, with
is an isomorphism of codes, with 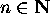 is
recursively unsolvable in n given arbitrary w,
is
recursively unsolvable in n given arbitrary w, 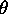 . The equation
. The equation
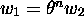 , with
, with 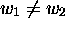 , is also recursively unsolvable in
n.
(
, is also recursively unsolvable in
n.
( ) Meeting of October 21, 1963.
) Meeting of October 21, 1963.
 ) N. CHOMSKY et M. P. SCHüTZENBERGER,
Computer Programming and Formal Systems, Hirschberg and Braffort,
North-Holland Publ. Co., Amsterdam, 1963, p. 118--161.
) N. CHOMSKY et M. P. SCHüTZENBERGER,
Computer Programming and Formal Systems, Hirschberg and Braffort,
North-Holland Publ. Co., Amsterdam, 1963, p. 118--161.
 ) H. WANG, Mathematische Annalen, 152,
1963, p. 65--74.
) H. WANG, Mathematische Annalen, 152,
1963, p. 65--74.
 ) M. MINSKY, Annals of Math., 74-3, 1961.
) M. MINSKY, Annals of Math., 74-3, 1961.
 ) M. P. SCHüTZENBERGER,
I. R. E. Trans. Inf. Theory, IT-2, 1956, p. 47-60.
) M. P. SCHüTZENBERGER,
I. R. E. Trans. Inf. Theory, IT-2, 1956, p. 47-60.
 ) E. POST, Amer. J. Math., 65, 1943,
p. 196--215.
) E. POST, Amer. J. Math., 65, 1943,
p. 196--215.
 ) E. POST, Bull. Amer. Math. Soc., 52,
1946, p. 264--268.
(Euratom, 51, rue Belliard, Bruxelles.)
) E. POST, Bull. Amer. Math. Soc., 52,
1946, p. 264--268.
(Euratom, 51, rue Belliard, Bruxelles.)


Next: About this document
Michael Frank
Tue Jan 13 23:35:18 EST 1998