Récursive insolubilité en
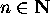 de
l'équation
de
l'équation 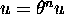 , où
, où 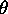 est un isomorphisme de
codes . Note (
est un isomorphisme de
codes . Note ( ) de M. Yves Lecerf, présentée par
M. André Lichnerowicz.
) de M. Yves Lecerf, présentée par
M. André Lichnerowicz.


Comptes Rendus Hebdomadaires des Séances de L'académie des Sciences, 257:2597--2600, Séance du 28 Octobre 1963.
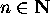 de
l'équation
de
l'équation 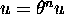 , où
, où 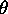 est un isomorphisme de
codes . Note (
est un isomorphisme de
codes . Note ( ) de M. Yves Lecerf, présentée par
M. André Lichnerowicz.
) de M. Yves Lecerf, présentée par
M. André Lichnerowicz.
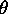 . Leurs propriétés
permettent de prouver que l'equation en
. Leurs propriétés
permettent de prouver que l'equation en 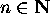 ,
, 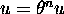 est
récursivement insoluble. Une second Note appliquera ceci à la
démonstration d'une conjecture de Schützenberger rattachant le
problème des correspondances de Post à des problèmes de
diagonalisation d'homomorphismes de monoïdes libres.
est
récursivement insoluble. Une second Note appliquera ceci à la
démonstration d'une conjecture de Schützenberger rattachant le
problème des correspondances de Post à des problèmes de
diagonalisation d'homomorphismes de monoïdes libres.
1. ISOMORPHISMES DE CODES, éPIMORPHISMES DE CODES. ---
a. Une conjecture de Schützenberger. --- Soient deux monoïdes
libres non triviaux 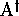 et
et 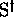 , soient deux
homomorphismes
, soient deux
homomorphismes 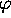 et
et 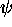 de
de 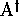 dans
dans 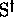 , et
soit le problème de la recherche de solutions non triviales
, et
soit le problème de la recherche de solutions non triviales 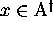 pour l'équation de diagonalisation
pour l'équation de diagonalisation 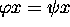 . Un
résultat de Post (
. Un
résultat de Post ( ) est que cette équation est récursivement
insoluble dans le cas de
) est que cette équation est récursivement
insoluble dans le cas de 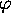 et
et 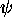 homomorphismes quelconques. Elle
l'est également lorsqu'on astreint
homomorphismes quelconques. Elle
l'est également lorsqu'on astreint 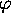 à être un monomorphisme;
Chomsky et Schützenberger ont fait observer, en effet (
à être un monomorphisme;
Chomsky et Schützenberger ont fait observer, en effet ( ), que ce cas
peut se ramener au Tag-problem de Post (
), que ce cas
peut se ramener au Tag-problem de Post ( ) lui-même récursivement
insoluble d'après un résultat de Minsky (
) lui-même récursivement
insoluble d'après un résultat de Minsky ( ). Schützenberger a
conjecturé que l'équation
). Schützenberger a
conjecturé que l'équation 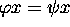 reste encore récursivement
insoluble quand à la fois
reste encore récursivement
insoluble quand à la fois 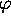 et
et 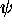 sont deux monomorphismes.
sont deux monomorphismes.
b. Isomorphismes de codes. --- Au lieu de 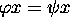 , il
revient au même de considérer l'équation
, il
revient au même de considérer l'équation 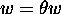 , où
, où
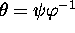 (ce qui est une notation abrégée pour dire
que
(ce qui est une notation abrégée pour dire
que 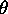 est une bijection de
est une bijection de 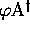 dans
dans 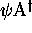 définie par
définie par 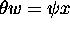 pour
pour 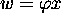 ). Par
facilité de langage, on appellera isomorphismes de codes
les applications telles que
). Par
facilité de langage, on appellera isomorphismes de codes
les applications telles que 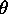 . Ce terme rappelle que
. Ce terme rappelle que
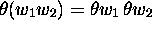 ; et aussi que,
; et aussi que, 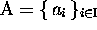 désignant l'alphabet (les générateurs)
de
désignant l'alphabet (les générateurs)
de 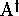 ,
, 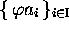 et
et 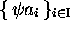 sont appelés des codes sur
sont appelés des codes sur 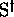 , car, pour y quelconque de
, car, pour y quelconque de 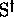 , il existe au plus un
ensemble d'indices
, il existe au plus un
ensemble d'indices 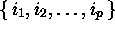 tels que
tels que 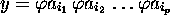 , et de même pour
, et de même pour 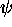 .
En fait, c'est surtout à l'étude des isomorphismes de code que seront
consacrées la présente Note et la suivante.
.
En fait, c'est surtout à l'étude des isomorphismes de code que seront
consacrées la présente Note et la suivante.
c. Définitions d' isomorphismes de codes
particuliers par donnée de relations. --- 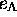 et
et 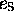 désignant les éléments neutres respectivement de
désignant les éléments neutres respectivement de 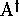 et de
et de
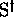 , il va de soi implicitement pour tout
, il va de soi implicitement pour tout 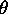 que l'on a
que l'on a
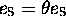 , avec
, avec 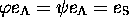 (d'où, d'ailleurs, une solution triviale pour
(d'où, d'ailleurs, une solution triviale pour 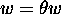 et pour
et pour
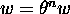 , avec
, avec 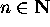 ). Ceci étant, chaque isomorphisme de
codes particulier pourra être défini par la donnée d'un ensemble de
relations du type
). Ceci étant, chaque isomorphisme de
codes particulier pourra être défini par la donnée d'un ensemble de
relations du type 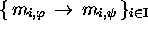 , à condition que
, à condition que 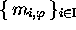 et
et
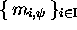 soient des codes
et que la correspondance soit bijective. En effet,
soient des codes
et que la correspondance soit bijective. En effet, 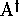 est
implicitement défini par
est
implicitement défini par 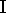 ,
, 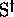 l'est par les symboles
utilisés pour noter les
l'est par les symboles
utilisés pour noter les 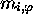 et
et 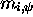 ; et l'on peut
interpréter les relations comme des correspondances
; et l'on peut
interpréter les relations comme des correspondances 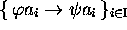 .
.
d. Vérification qu'un ensemble de mots donnés est un code. ---
Plus loin, on invoquera souvent la propriété suivante : Si  et
et
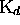 désignent respectivement un code et un préfix-code droit
sur
désignent respectivement un code et un préfix-code droit
sur 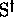 , et si
, et si 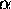 est un symbole (générateur de
est un symbole (générateur de 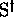 ) ne figurant pas dans
) ne figurant pas dans  ni dans
ni dans 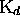 , alors,
l'ensemble
, alors,
l'ensemble 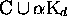 est un code. De même, en
remplaçant
est un code. De même, en
remplaçant 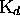 par un préfix-code gauche
par un préfix-code gauche 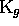 ,
l'ensemble
,
l'ensemble 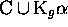 est un code. Rappelons que tout
préfix-code droit
est un code. Rappelons que tout
préfix-code droit 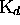 est par définition (
est par définition ( ) tel que, si
) tel que, si
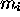 ,
, 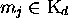 et si, avec
et si, avec 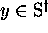 , on a
, on a 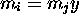 ,
alors,
,
alors, 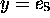 (tandis que pour les préfix-codes gauches, c'est
(tandis que pour les préfix-codes gauches, c'est
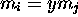 qui impose
qui impose 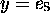 ).
).
e. Épimorphismes de codes. --- On parlera d'
épimorphisme de codes 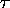 dans le cas de relations
dans le cas de relations
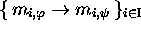 , où
, où
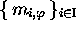 est bien un code
est bien un code 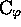 , mais
où
, mais
où 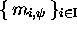 est astreint seulement à ne pas
contenir d'autres mots que ceux d'un code
est astreint seulement à ne pas
contenir d'autres mots que ceux d'un code 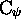 .
MACHINES DE TURING RéVERSIBLES. --- Soit une machine de
Turing MT dont
.
MACHINES DE TURING RéVERSIBLES. --- Soit une machine de
Turing MT dont 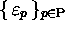 et
et
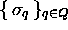 sont les ensembles d'états et de symboles, et
sont les ensembles d'états et de symboles, et
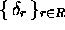 les déplacements de ruban, qui peuvent être
les déplacements de ruban, qui peuvent être
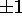 ou 0. On peut définir MT par un
ensemble de quintuples
ou 0. On peut définir MT par un
ensemble de quintuples
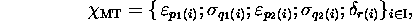
où les indices 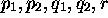 sont fonctions de l'indice i. A
chacun de ces quintuples, décidons d'associer un quintuple image
inverse (
sont fonctions de l'indice i. A
chacun de ces quintuples, décidons d'associer un quintuple image
inverse (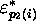 ;
; 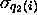 ;
;
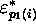 ;
; 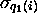 ;
; 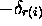 ). L'ensemble
de ceux-ci ne constituera généralement pas une machine de Turing; mais
lorsqu'il en sera ainsi, on dira que MT est réversible ,
et l'on donnera à la nouvelle machine le nom d'image inverse MT
). L'ensemble
de ceux-ci ne constituera généralement pas une machine de Turing; mais
lorsqu'il en sera ainsi, on dira que MT est réversible ,
et l'on donnera à la nouvelle machine le nom d'image inverse MT de
MT. Les
de
MT. Les 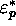 seront dits images des
seront dits images des 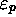 . La
substitution d'un
. La
substitution d'un 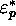 à un
à un 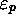 dans une
configuration instantanée
dans une
configuration instantanée 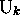 sera dite passage à
sera dite passage à 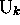 à sa configuration image
à sa configuration image 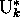 . Les suites de configurations de
. Les suites de configurations de
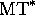 sont images de celles de MT, mais
sont images de celles de MT, mais 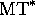 les parcourt
dans l'ordre inverse. Considérons maintenant la machine R (MT), dont
l'ensemble de quintuples est
les parcourt
dans l'ordre inverse. Considérons maintenant la machine R (MT), dont
l'ensemble de quintuples est
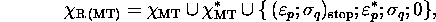
où
Preuve. --- On montre comment passer de
b. THéORèME 1. --- Le problème du stop pour
une machine de Turing réversible générale est indécidable. Il en
est de même du problème du retour à la configuration initiale, et de
celui du passage par une configuration déterminée autre que la
configuration initiale.
c. THéORèME 2. --- L'équation
(
(
(
(
(
(
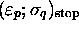 désigne tout couple pour
lequel MT stoppe. Si l'on fait partir MT et R(MT) d'une même
configuration instantanée
désigne tout couple pour
lequel MT stoppe. Si l'on fait partir MT et R(MT) d'une même
configuration instantanée 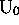 , elles passent par les mêmes
configurations tant que MT ne stoppe pas (donc éventuellement
indéfiniment). Lorsque MT stoppe, R(MT) continue, parcourt en ordre
inverse les configurations images des configurations parcourues, et passe
par l'image de la configuration initiale. R(MT) sera dite couplage de MT
avec son image inverse.
REPRéSENTATION DE MACHINES DE TURING PAR DES éPIMORPHISMES
(OU DES ISOMORPHISMES) DE CODES. --- Revenons au cas où MT est
quelconque. A chacun de ses quintuples comportant le mouvement +1, soit
par exemple
, elles passent par les mêmes
configurations tant que MT ne stoppe pas (donc éventuellement
indéfiniment). Lorsque MT stoppe, R(MT) continue, parcourt en ordre
inverse les configurations images des configurations parcourues, et passe
par l'image de la configuration initiale. R(MT) sera dite couplage de MT
avec son image inverse.
REPRéSENTATION DE MACHINES DE TURING PAR DES éPIMORPHISMES
(OU DES ISOMORPHISMES) DE CODES. --- Revenons au cas où MT est
quelconque. A chacun de ses quintuples comportant le mouvement +1, soit
par exemple 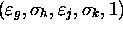 , on
associe trois relations, à savoir ici :
, on
associe trois relations, à savoir ici :
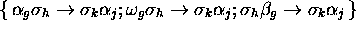 .
Aux
.
Aux 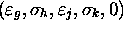 , on associe :
, on associe :
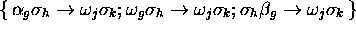 .
Aux
.
Aux 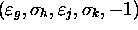 , on associe
, on associe
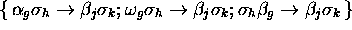 .
Enfin, à tout symbole
.
Enfin, à tout symbole 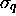 de MT, on associe
de MT, on associe
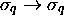 . On peut vérifier, par le procédé
donné au paragraphe 1, d, que l'ensemble de toutes ces relations
définit un épimorphisme de codes. Soit
. On peut vérifier, par le procédé
donné au paragraphe 1, d, que l'ensemble de toutes ces relations
définit un épimorphisme de codes. Soit 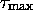 celui-ci,
celui-ci,
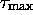 est une représentation de MT, car il en définit
l'alphabet et les quintuples. On peut, d'autre part, trouver pour les
configurations instantanées de MT des notations telles que pour tout
couple de configurations successives
est une représentation de MT, car il en définit
l'alphabet et les quintuples. On peut, d'autre part, trouver pour les
configurations instantanées de MT des notations telles que pour tout
couple de configurations successives 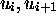 on ait
on ait
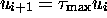 . Pour cela, une configuration se composera
d'une suite de symboles
. Pour cela, une configuration se composera
d'une suite de symboles 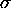 (le mot du ruban) dans laquelle on
intercalera une des lettres
(le mot du ruban) dans laquelle on
intercalera une des lettres 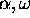 ou
ou 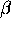 , avec un indice p
égal à celui de l'état
, avec un indice p
égal à celui de l'état 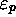 de la machine, et de façon
à indiquer, non seulement la position
de la machine, et de façon
à indiquer, non seulement la position 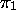 du prochain symbole à
lire, mais encore celle
du prochain symbole à
lire, mais encore celle 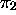 du symbole précédemment écrit (acev
convention particulière pour la configuration initiale). Un
du symbole précédemment écrit (acev
convention particulière pour la configuration initiale). Un 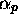 signifie que
signifie que 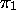 est le premier symbole à sa droite,
est le premier symbole à sa droite, 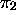 le
premier à sa gauche. Un
le
premier à sa gauche. Un 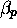 , l'inverse. Un
, l'inverse. Un 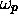 signifie
que
signifie
que 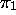 et
et 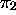 , confondus, sont tous deux le premier symbole à
droite de ce
, confondus, sont tous deux le premier symbole à
droite de ce 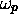 . On a bien alors
. On a bien alors 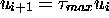 . Si
certains états
. Si
certains états 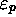 ne peuvent apparaître que sous deux
seulement, ou une seule, des formes
ne peuvent apparaître que sous deux
seulement, ou une seule, des formes 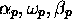 , et soit
, et soit
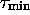 obtenu en retranchant de
obtenu en retranchant de  toutes les
relations contenant des formes qui n'apparaissent jamais, alors,
toutes les
relations contenant des formes qui n'apparaissent jamais, alors, 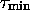 est encore tel que
est encore tel que 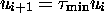 . Si
. Si 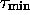 est un isomorphisme de codes, MT est réversible.
SIMULATION DE MT QUELCONQUE SUR
est un isomorphisme de codes, MT est réversible.
SIMULATION DE MT QUELCONQUE SUR 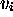 ) sur une machine de Turing réversible
) sur une machine de Turing réversible 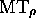 (de
configurations
(de
configurations 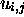 ) de façon que :
) de façon que : 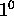 quand MT passe de
quand MT passe de 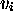 à
à 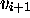 ,
, 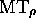 passe de
passe de 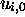 à
à 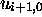 par
l'intermédiaire d'un nombre fini de configurations
par
l'intermédiaire d'un nombre fini de configurations 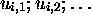 ;
; 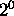 on passe d'un
on passe d'un 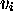 au suivant par un épimorphisme de
codes
au suivant par un épimorphisme de
codes 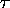 , d'un
, d'un 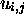 au suivant par un isomorphisme de codes
au suivant par un isomorphisme de codes
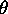 ;
; 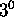 si les configurations initiales sont
si les configurations initiales sont 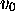 pour MT et
pour MT et
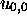 pour
pour 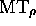 , avec
, avec 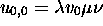 , alors
pour tout i, on a
, alors
pour tout i, on a 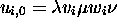 , où
, où 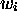 est un
mot, et où
est un
mot, et où 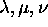 sont trois symboles qui n'apparaissent ni
dans
sont trois symboles qui n'apparaissent ni
dans 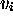 ni dans
ni dans 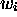 , si bien que
, si bien que 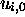 connu donne
connu donne 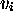 et
et 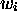 ;
;
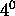 il y a des symboles
il y a des symboles 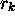 dont chacun représente une relation de
dont chacun représente une relation de
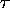 autre que d'identité; un symbole blanc b; et pour tout i on a
autre que d'identité; un symbole blanc b; et pour tout i on a
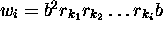 , où
, où 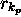 est la relation
intervenue dans
est la relation
intervenue dans 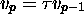 . Ainsi,
. Ainsi, 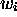 représente l'histoire
du calcul de MT jusqu'au temps i;
représente l'histoire
du calcul de MT jusqu'au temps i; 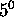
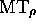 stoppe sur les
stoppe sur les
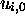 correspondant à des stop de MT, et eux seulement;
correspondant à des stop de MT, et eux seulement; 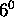 la
machine
la
machine 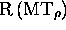 , couplage de
, couplage de 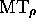 avec son
image inverse, partie de
avec son
image inverse, partie de 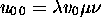 passe par la
configuration image
passe par la
configuration image 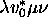 si et seulement si MT, partie de
si et seulement si MT, partie de
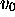 , stoppe;
, stoppe; 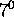 il existe pour
il existe pour 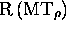 certaines
configurations instantanées
certaines
configurations instantanées 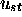 telles que, partant de
telles que, partant de 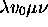 ,
, 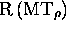 ne peut atteindre ces configurations
autrement qu'en passant par
ne peut atteindre ces configurations
autrement qu'en passant par 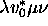 (c'est-à-dire si MT,
partie de
(c'est-à-dire si MT,
partie de 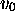 , stoppe). On peut ainsi faire en sorte que le retour de
, stoppe). On peut ainsi faire en sorte que le retour de
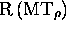 à
à 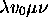 (ou bien, le passage par des
(ou bien, le passage par des
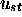 encadrés par
encadrés par 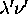 au lieu de
au lieu de 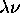 ) soit
conditionné par un stop de MT.
) soit
conditionné par un stop de MT.
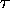 , supposé donné
par un ensemble de relations
, supposé donné
par un ensemble de relations 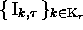 à l'ensemble des relations
à l'ensemble des relations 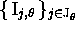 définissant
définissant 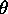 et
et 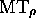 . Limitons-nous à
donner le principe de cette construction, en montrant comment simuler une
instruction
. Limitons-nous à
donner le principe de cette construction, en montrant comment simuler une
instruction 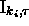 de la forme
de la forme
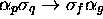 . A celle-ci, on associera :
une instruction
. A celle-ci, on associera :
une instruction
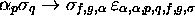 ,
où le symbole
,
où le symbole 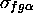 marque la place où l'on doit modifier
marque la place où l'on doit modifier
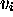 , et la nature de la modification; des instructions permettant de
conduire le contrôle à gauche de
, et la nature de la modification; des instructions permettant de
conduire le contrôle à gauche de  par un état
par un état
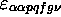 ; une instruction
; une instruction
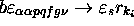 , où
, où
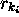 représente
représente 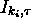 , complètant
, complètant 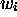 ; des instructions
de service déplaçant
; des instructions
de service déplaçant  et, éventuellement aussi
et, éventuellement aussi 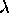 ,
, 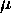 et
et 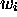 tout entier, pour rétablir les blancs nécessaires dans
tout entier, pour rétablir les blancs nécessaires dans
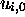 puis reportant le contrôle en
puis reportant le contrôle en 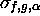 avec un
état
avec un
état 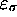 ; une instruction
; une instruction
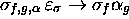 qui
complète
qui
complète 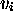 dans
dans 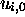 .
.
 , où
, où 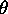 est un isomorphisme de codes, avec
est un isomorphisme de codes, avec 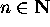 est
récursivement insoluble en n pour w,
est
récursivement insoluble en n pour w, 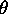 donnés quelconques.
L'equation
donnés quelconques.
L'equation 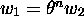 , avec
, avec 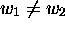 , est aussi
récursivement insoluble en n.
(
, est aussi
récursivement insoluble en n.
( ) Séance du 21 octobre 1963.
) Séance du 21 octobre 1963.
 ) N. CHOMSKY et M. P. SCHüTZENBERGER,
Computer Programming and Formal Systems, Hirschberg et Braffort,
North-Holland Publ. Co., Amsterdam, 1963, p. 118--161.
) N. CHOMSKY et M. P. SCHüTZENBERGER,
Computer Programming and Formal Systems, Hirschberg et Braffort,
North-Holland Publ. Co., Amsterdam, 1963, p. 118--161.
 ) H. WANG, Mathematische Annalen, 152,
1963, p. 65--74.
) H. WANG, Mathematische Annalen, 152,
1963, p. 65--74.
 ) M. MINSKY, Annals of Math., 74-3, 1961.
) M. MINSKY, Annals of Math., 74-3, 1961.
 ) M. P. SCHüTZENBERGER,
I. R. E. Trans. Inf. Theory, IT-2, 1956, p. 47-60.
) M. P. SCHüTZENBERGER,
I. R. E. Trans. Inf. Theory, IT-2, 1956, p. 47-60.
 ) E. POST, Amer. J. Math., 65, 1943,
p. 196--215.
) E. POST, Amer. J. Math., 65, 1943,
p. 196--215.
 ) E. POST, Bull. Amer. Math. Soc., 52,
1946, p. 264--268.
(Euratom, 51, rue Belliard, Bruxelles.)
) E. POST, Bull. Amer. Math. Soc., 52,
1946, p. 264--268.
(Euratom, 51, rue Belliard, Bruxelles.)


Next: About this document
Michael Frank
Tue Jan 13 23:20:32 EST 1998