[About the Foresight Institute] [Index of Foresight Conferences]

[Index of Papers]

WARNING: This page uses the <sup> and <sub> convention for superscripts and subscripts, as specified in the HTML 3.2 Reference Specification. If "10³" is the same as "103" then your browser does not support superscripts. If "x_i" is the same as "xi" then your browser does not support subscripts. Failure to support superscripts or subscripts can lead to confusion in the following text, particularly in interpreting exponents. We also use the ISO Latin-1 Character Entities from that same specification.

Although a complete nanotechnology does not yet exist, we can already foresee some new directions in theoretical computer science that will be required to help us design maximally efficient computers using nano-scale components. In particular, we can devise novel theoretical models of computation that are intended to faithfully reflect the computational capabilities of physics at the nano-scale, in order to serve as a basis for the most powerful possible future nanocomputer architectures.

In this paper we present arguments that a reversible 3-D mesh of processors is an optimal physically-realistic model for scalable computers. We show that any physical architecture based on irreversible logic devices would be asymptotically slower than realizations of our model, and we argue that no physical realization of computation aside from quantum computation could be asymptotically faster.

We also calculate, using parameters from a variety of different existing and hypothetical technologies, how large a reversible computer would need to be in order to be faster than an irreversible machine. We find that using current technology, a reversible machine containing only a few hundred layers of circuits could outperform any existing machine, and that a reversible computer based on nanotechnology would only need to be a few microns across in order to outperform any possible irreversible technology.

We argue that a silicon implementation of the reversible 3-D mesh could be valuable today for speeding up certain scientific and engineering computations, and propose that the model should become a focus of future study in the theory of parallel algorithms for a wide range of problems.

1. Introduction

The prospect of molecular manufacturing technology has suggested a number of intriguing possibilities for the design of extremely small, fast, and energy-efficient digital logic devices that could be used as the basis of future computers. It is not yet clear which of the variety of proposed new device technologies will ultimately prove most useful. However, any future computing technology must, of course, obey the fundamental constraints that the laws of physics impose on the manipulation of information. As our computer components approach the nano-scale, these constraints become ever more apparent and important as factors that limit computer performance.

It would be useful to have theoretical models of information processing that could tell us, at least in broad terms, how to achieve the maximum computational efficiency that is possible given the laws of physics. Such a model could serve as the basis for the design of highly efficient computer architectures, and of efficient algorithms to run on them. If the model is to some degree independent of the particular device technology, then its architectures and algorithms can be reused across a wide range of device technologies, performing well all the way down to the nanometer realm. It is the intent of this paper to outline such a model.

Some physical constraints, such as the fact that the speed at which information can travel is bounded above by a constant (the speed of light), are already reflected in existing computer designs and in some models of computation. In this paper, we push further ahead, and focus on the additional implications of another constraint, namely the second law of thermodynamics, which states that entropy cannot be destroyed. This law can be viewed as a consequence of the reversibility of microscopic physical dynamics.

Traditional computer designs already cope with thermodynamic issues to some extent; the cooling of computer systems is already a major concern. However, we argue that traditional logic devices and models of computation, all of which involve the irreversible production of some minimum amount of entropy per operation, are fundamentally flawed, in that they fall short of permitting the maximum computational efficiency that is possible within the second law. We describe an alternative class of machines based on asymptotically reversible logic devices which entail no minimum entropy per operation, organized in a way that permits arbitrary patterns of logically reversible information processing in 3-dimensional space. We argue that given one or two reasonable additional constraints, a large and important class of computations, including many useful simulations of physical systems, can be performed more rapidly at sufficiently large scales on these 3-D reversible machines than on any physically possible computer based on irreversible primitive operations. For other computations, we argue that our 3-D reversible architecture is, roughly speaking, at least as fast as any possible alternative (neglecting quantum coherent computers).

A reversible architecture like we describe can already be implemented in today's semiconductor technology using reversible circuit techniques, and we project that at an achievable scale, the machine would be faster than any irreversible computer built using the same VLSI fabrication process. But future irreversible technologies may be much more thermodynamically efficient than present ones. In order to beat the best possible irreversible technology, a reversible machine built using present technology would have to be astronomically large. But nanotechnologists and others have proposed a variety of very small-scale and highly efficient asymptotically reversible device technologies. As the efficiency of the best available reversible technology improves, the scale at which reversible architectures will be faster than the best possible irreversible technology will continue to decrease. In this paper we derive the appropriate scaling relations, and present numerical estimates of the scales at which different nanotechnological and electronic reversible technologies will be capable of faster speeds than the best-existing and best-possible irreversible technologies.

2. Physical Constraints

In this section we briefly summarize the various physical constraints on information processing that we know about, and their implications for the structure of the optimal architecture.

2.1. Velocity Limit. As we all know, special relativity implies that information cannot propagate faster than the speed of light, c = 299,792,458 m/s. This fact has an important effect on the speed of large-scale processors. A typical propagation delay for a logic gate built with fairly recent 1.2 µm CMOS technology is on the order of 200 ps (Rabaey 1996, p. 136), during which time information can travel at most 6 cm even if it is transmitted by the fastest possible means (e.g. optically through free space). In practice, electrical transmission of signals along wires is slower than the speed of light, by a factor of around 2. Even worse, propagation delays along dissipative wires actually scale up in proportion to the square of the distance, unless the signals are periodically re-generated by additional buffering logic.

So, a computer does not need to be very large before delays due to communication of information across it surpass the delays due to some minimal amount of processing of that information. Any time a signal travels a more than a certain distance, one can insert some amount of processing of that signal along its path without slowing it down significantly. For example, the signal can be examined to see if it needs to be rerouted in a different direction or processed further. Thus it makes sense for some amount of logic to appear periodically in all directions along which signals may travel.

This line of argument leads eventually to the realization that at some sufficiently large scale, the optimal organization of a general-purpose parallel computer is as a mesh, an array of processing units of some size packed together and directly communicating only with their nearest neighbors. In the optimal organization, each processing unit will have a diameter comparable to the maximum distance a signal can travel within the time required for some reasonable minimal amount of processing of a signal, for example to determine how it should be routed or whether it should be processed further. Internally to each processing unit, a non-mesh architecture may be favored, since at that smaller scale, communication times will be short compared to the cost of computation. Detailed arguments for mesh architectures can be found in (Vitányi 1988, Bilardi and Preparata 1993).

It is important to realize that the optimality of mesh architectures does not yet make itself felt much in current multiprocessor designs, because the optimal scale of the mesh elements would be too large. Even if it only takes 10 or so gate delays to perform some minimal useful amount of processing of a signal, with today's technology that corresponds to a time of several nanoseconds, during which an efficiently propagated signal may travel several feet, suggesting that mesh elements have about that diameter. Moreover, a machine will need to contain a fair number of mesh elements before the advantages of the mesh organization become significant compared to competing topologies. So we are talking about a fairly large computer.

However, as the technology for logic devices improves, the mesh architecture will become important at smaller and smaller scales. For example, Konstantin Likharev's group at SUNY has developed superconducting integrated circuits based on Josephson junctions that operate at clock speeds over 100 GHz (Likharev 1996). At such rates, the distance light can travel per cycle is only around 3 mm, which means that a reasonable number of mesh elements of that size may be integrated on a single 1 cm chip, and the advantages of the mesh architecture will begin to become apparent. And if, as we expect, future nanomanufacturing technology permits the efficient construction of 3-dimensional logic arrays of much larger sizes, the mesh design will be even more advantageous.

Mesh architectures are desirable not only because of the arguments as to their optimality for large scale computing, but because they are simple and regular and relatively straightforward to program. Designing algorithms for mesh architectures is somewhat similar to the task of realizing some desired hardware functionality using real components that are arranged in 3-D space, a skill that computer designers already have expertise at.

Let us move on to some other physical constraints.

2.2. Three-Dimensionality of Space. Our universe has three spatial dimensions; this has implications for the structure of the optimal computer architectures. Together with the speed-of-light bound on the transmission of information, it implies that the volume of space to which a piece of information can possibly travel in a time t grows as O(t³), that is, at most in proportion to t³. This implies that any interconnection scheme that connects a processor to more than order n³ others in only n steps is not physically realizable with constant-time steps. Meshes therefore cannot have more than three dimensions. In principle, meshes having 3 dimensions can compute fastest; for example, sorting of n elements can be performed in O(n^1/3) time on a 3-D mesh but requires at least order n^1/2 time on a 2-D mesh (Leighton 1992, §1.9, pp. 229-232; §1.6.4, pp. 151-153). Results such as these would seem to suggest that the 3-D version of the mesh is optimal. However, there are some other physical constraints that must be taken into account, before we come to any firm conclusions.

2.3. Limited Information Capacity. Fundamental quantum-mechanical arguments appear to dictate a particular finite upper bound on the amount of information and entropy (unknown information) that can be contained in a region of space, as a function of the region's size and the amount of energy contained within it. The bound appears to apply no matter what kind and arrangement of physical entities are used to encode the information. (Bekenstein 1984).

Thus, no matter what technology is used, the amount of information or entropy contained in a computer of bounded size cannot increase indefinitely, unless the amount of energy within it increases indefinitely as well. Even if there were no more immediate bounds on energy, we know from general relativity that any system of bounded size will collapse into a black hole if it contains more than a critical amount of energy. Thus, there seems to be a fundamental limit to how many bits can be stored in a computer of given size.

Of course, any particular technology for the foreseeable future will have its own much stricter limits on the density with which information and entropy can exist within it. Entropy densities above a certain level in any known material will cause the material to melt. Information densities in an electromagnetic signal are limited as a function of the available power.

The important implication of all this for computer design is that if a computation is generating new bits of information/entropy at any nonzero net rate, eventually the capacity to store those bits within the computer's physical volume will be exceeded, and the computation can only proceed if bits exit through the computer's surface. But if bits can only exist at some maximum spatial density 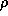(in units of, for example, bits per unit volume), and the maximum speed at which information can travel is v (which is at most c), then this implies that the maximum flux F of bits per second per unit area through any surface is



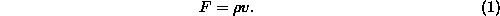
Thus, if the area of the smallest surface (the convex hull) that fully encloses some region of space is A, then the maximum sustainable net rate R at which information can be generated within that region is

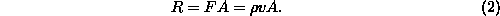
Thus, if new bits of information are being generated continually as a computer runs, at some fixed quantity per operation, without somehow being reclaimed or recycled so that the net rate of bit generation is zero, then the computer's rate of operation will be limited to being proportional to the area A of its convex hall. In such a case, increasing the thickness of a computer beyond a certain point is effectively useless, and so one might as well stick with a two-dimensional mesh architecture at large scales.

This issue could be circumvented if the net generation of information per operation could be avoided, or reduced arbitrarily. This brings us to the final physical constraint of relevance to our discussion.

2.4. Reversibility of physics. The various systems of mechanics that form the basis of physics all have the property of reversibility, that is, they are deterministic in the reverse time direction (and incidentally in the forwards time direction as well). This includes all of classical mechanics, relativistic mechanics, quantum mechanics, quantum field theories, and general relativity. (It is a popular misconception that quantum mechanics is nondeterministic. In quantum theory, all systems are perfectly deterministic at the level of the unitary evolution of the quantum wavefunction. The apparent nondeterminism that we observe can be interpreted as an emergent phenomenon predicted by the underlying deterministic theory.) Reversibility is an essential property of all of these systems; our understanding of physics would have to completely change in order to accommodate any irreversibility occurring at a fundamental level. The physics of black holes, as currently conceived, seems to imply irreversible information destruction, but the situation is not very well understood, and the issue is still being actively debated (Preskill 1992, Mashkevich 1997, Englert 1997). In any case, there seems to be a general consensus among physicists that reversibility is maintained in all areas of mechanics not involving extreme cases such as black holes.

The reversibility of physics implies that no physical state can be reached by more than one path, since otherwise the reverse evolution would be nondeterministic. No physical mechanism can exist which will reach a single state from either of two distinct predecessors. So a bit of information that is stored in a computer cannot truly be erased, because this would imply the convergence of two distinct states into one. As physicists like to say, ``state space is incompressible.'' Instead, when a computer ``erases'' a bit, the information about the previous value of the bit is merely moved, out of the computer's logical state, and into the thermal state of the computer and its environment. The bit is lost to us, but it is still present in the form of entropy (uncontrolled, inaccessible information).

Therefore, a computer such as those we have today, that constantly ``irreversibly erases'' temporary results it has generated, is actually constantly generating new entropy. Because of the reversibility of physics, the entropy cannot be removed once it has been created, since that would cause distinct states to irreversibly merge. (This implies the second law of thermodynamics, which states that total entropy of a closed system can never decrease.) So there is a net production of new entropy information in our computer, and so it is subject to the constraints on information/entropy flux derived above, which imply that the computer cannot make effective use of the third dimension, beyond a certain point, to speed up computation. We will analyze this situation in more detail in §4.

2.5. Energy cost of information dissipation. In the previous subsection we stated that ``erasing'' a bit in a normal computer just means moving that bit from being an explicit piece of computational state to being part of the microscopic thermal state of the computer and its environment. Now we review the physical implications for the amount of energy that must be dissipated in this process, although they are not required for the main results in this paper.

For each possible state the thermal system may have before the bit is erased, it must have at least two different possible states after the bit is erased, one for each value of the bit. The size N of the thermal system's accessible state space must therefore be doubled to accommodate the new information; the natural logarithm S = ln(N) of the size of the state space, also called the entropy, is incremented by an amount ln(2) = 0.69..., which we may call 1 bit of entropy. Generally, the only way to increase the size of a thermal system's accessible state space (other than by directly increasing the system's volume) is to add energy to the system. The amount of extra energy required scales in proportion to the increase in entropy, at least for small increases in entropy. The constant of proportionality is called the temperature of the system.

The above is a perfectly valid definition of temperature in terms of energy and numbers of states. We can state, as a definition:



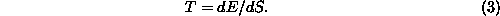
Our rather arbitrary unit of temperature called the Kelvin can itself be defined as the temperature at which 1.3806513 × 10^-23 J of energy is required to increase the natural log S of the state count by 1. Since the Kelvin is the standard unit of temperature, and since dS = dE/T, the entropy S is standardly expressed in units of Joules per Kelvin, rather than in bits or in dimensionless natural log units (which we may call nats). Boltzmann's constant k_B = 1.3806513 × 10^-23 J/K is just 1 nat of entropy, expressed in more traditional units.

From all this, it just falls out immediately that the amount of energy E that needs to be put into a thermal system in order to double its number of states is just



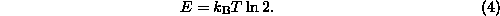
The k_B is just 1 nat of entropy, ln 2 is the number of nats in a bit, so k_B ln 2 expresses 1 bit's worth of entropy. Multiplying by the temperature just converts this entropy to the amount of energy required to add it to a system at that temperature.

All this implies the much-discussed result that erasing a bit of information in a computer requires dissipating at least k_BT ln 2 energy. This is just because physics is reversible, so the bit must be moved elsewhere rather than being destroyed, and k_BT ln 2 is just the energy required to add a bit of information to a heat bath at temperature T, by the very definition of temperature! The relationship between bit erasure and energy dissipation was apparently first described by Landauer (1961).

Note that since T is the temperature of the heat bath where the information finally ends up, not the temperature of the device that held the information originally, cooling a computer cannot decrease the total energy dissipation required to erase bits, if the dissipation in the cooling system is taken into account. The entropy that is generated does not build up indefinitely in the cooling system (or it would not stay cool), instead it ultimately ends up in some natural thermal reservoir in the environment. The coolest thermal reservoir of effectively unlimited capacity that we have available is the interstellar microwave background, at a temperature of 3 K. Thus, no process that generates entropy can in the long run sustain an energy dissipation cost less than k_B 3 K ln 2 = 3 × 10^-23 J per bit generated, and this can only be attained if the entropy is transmitted directly into space. For systems that use the atmosphere as their thermal reservoir, the temperature is around room temperature or 300 K, for a minimum energy dissipation per bit of 2.9 × 10^-21 J.

The above analysis just gives the minimum energy dissipation for bit erasure, which holds only if the bit is discarded without any other bits of entropy being generated. But the most energy-efficient electronic digital logic gates currently available in commercial VLSI CMOS fabrication processes store bits on circuit nodes of capacitances of around 30 fF, at a potential of 1 V or more. All of the energy E = ½CV² = 1.5 × 10^-14 J that is stored in these circuits is dissipated to heat whenever the device switches and an old result is lost, thus generating at least E / k_BT ln 2 = 1.7 × 10⁶ bits of new entropy, given that the chip must be operated at a temperature below the melting point (933.52 K) of the aluminum wires etched on it.

2.6. Maximum rate of state change. Although it is not directly relevant to the later points in this paper, it is interesting to note that quantum mechanics implies a strict upper limit to the frequency with which any physical system can transition from one distinguishable state to another. This limit is proportional to the total energy E of the system above its ground state energy E₀ (Margolus and Levitin 1996):



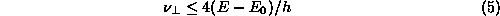
where h is Planck's constant, 6.6260755 × 10^-34 J/Hz. So, for example, an isolated subsystem consisting of a single electron at a potential of 1 V above its ground state contains just 1 eV of energy and therefore can never change state more rapidly than a rate of 4 eV / h = 1 PHz, or once per femtosecond.

Is is not clear whether the rate of state change given by this bound can in general actually be achieved as the rate at which useful computational operations are performed in a computer. But it seems to be an upper bound on this rate, at least.

This concludes our discussion of the various fundamental physical constraints and their immediate implications. Now in the following sections, we will see how the recycling of bits in asymptotically reversible logic devices arranged in a reversible architecture can better make use of three dimensional space.

3. Reversibility, Information and Entropy

In previous sections we mentioned concepts such as reversibility, information, and entropy, but did not relate them precisely. In this section, we attempt to put the definitions and interactions of these concepts on a somewhat firmer ground, as a basis for further discussion.

3.1. Reversibility and local reversibility. As already stated, a system is said to be reversible if it is deterministic when run in reverse. This definition can apply to physics, with its apparently continuous time, and also to systems that update their state at discrete time steps, such as a typical model of a computer. For the discrete case, a reversible system can be defined simply as a system in which each state can only have a single possible predecessor state, within the model.

But for purposes of avoiding entropy, this is not the whole story. We would like to evolve one computational state to the next using some physically reversible process. According to the previous definition, a computer is reversible automatically if it simply keeps its input around, because then, at any step in the computation, only a single predecessor state will be consistent with that input (given that the computation is deterministic). But determining whether a state is consistent with a stored input is something that in general requires a global examination of the state, and a long computation; for example, re-running forwards from the initial state to see if we arrive at a particular predecessor. Physical mechanisms, on the other hand, operate locally.

Therefore, we will be interested in computational models that are not only reversible but locally reversible, meaning that every individual logical operation, acting locally on a small part of the computer's state, should be reversible in and of itself. In other words, the local state after the operation is performed should completely determine what the local state was prior to the operation, without any need to look at some other part of the computer's state.

Locally reversible serial models of computation (in the form of reversible Turing machines) were first shown to be universal by Lecerf (1963) and later independently by Bennett (1973). Locally reversible parallel models (reversible cellular automata) were shown to be universal for parallel computations of lower dimensionality by Toffoli (1977). Reversible bounded-degree circuit models were explored by Toffoli (1980) and Fredkin and Toffoli (1982).

3.2. Information. For purposes of this paper, we will informally identify the information in a computational system as consisting of those bits of the system's state that are actually being used to represent something meaningful. This is in contrast to those bits of state corresponding to regions of memory that are currently unused, or to aspects of the computer's mechanical state that are unrelated to the computational state being represented. Under this definition, the amount of information in a system can increase or decrease over time, as more or less memory is used to represent things. Much of the information in the system will be redundant, because it is just derived from other information, but we still consider it information from the point of view of this definition.

Even in a reversible system, the amount of information can change over time if regions of memory that are currently unused are always kept in some known, canonical state, for example, all zero. Then, new meaningful results can be reversibly written in the unused space, and old results that are no longer needed can be unwritten to free up the space and change it back to zero, using, for example, an operation that is the reverse of the operation that generated the result to begin with.

The spirit of this definition of information can be extended to an arbitrary physical system, by identifying the information in the system as consisting of the states of all the pieces of the system that are not in some common canonical state (such as, for example, empty space).

3.3. Entropy. Entropy can be defined as a special case of information. Consider an arbitrary reversible physical system that produces some new derived information in such a way that the reverse operation that would underive that information can no longer be effectively applied. For example, suppose the redundant information is moving apart from the information that it was derived from, and the motion cannot be turned around in order to bring the two pieces of information together and cancel one of them out. Or, perhaps the information is still nearby, but it has become mixed up with a part of the system whose state is unknown or uncontrolled.

If, through circumstances such as these, some information produced by a system is never un-derived, then we can call this information entropy. Since by definition it is never underived, then its amount always increases over time, in any system that is reversible and thus can only remove information by underiving it. (In a non-reversible system, the amount of entropy in the system could be decreased by just irreversibly erasing some of the entropy instead.)

We propose that this definition of entropy, despite being somewhat informal, can be fruitfully identified both with Maxwell's concept of physical entropy, and also with Shannon's concept of the entropy in a signal.

As an example of the correspondence with Maxwellian entropy, when two different fluids are permitted to diffuse together, new information is created that specifies the exact pattern of how the molecules are mixed together, and this information is entropy to us, by our definition, because we have no way to get rid of it. Any known method of separation of the fluids will just move the new information somewhere else, rather than underiving it. However, suppose, as a thought experiment, that we discovered a way to exactly reverse the velocities and spins of all the particles in the fluid at once, and suppose that in other respects, the fluid is perfectly isolated from the outside world. Then the mixing process would reverse itself, all the information generated during the mixing would be underived, and the fluid would return to its initial separated state. This would not mean that entropy was decreasing during this process, but rather, that our earlier analysis was mistaken, and the information that was generated when the mixing first occurred was not entropy after all, because we had the capability to underive it. The definition of which information is entropy, and which information isn't, is relative to one's capabilities.

As for the information contained in a signal, it can be considered entropy if it is never going to be brought back together with and underived from the information at the source from which it was generated. However, if some of the information in the signal is correlated with other information in the signal, for example if we use a redundant encoding, or some long patterns occur frequently, then the redundant part of the information in the signal is not entropy, because it can be underived from the other information in the signal with which it is correlated, transforming the message into a more compact representation that is comprised of fewer raw bits of information. However, if the signal might just be dissipated rather than compressed, then no such underiving is done, and all of the information in the signal, even though it is redundant, it potentially entropy.

We assert that physical, thermal entropy and digital, computational entropy are really the same thing. This can be shown by observing that they are interconvertible. Entropy that is in the form of digital computer data can be transformed into thermal entropy by just letting it dissipate. In current technologies, this process inefficiently generates many additional bits' worth of new entropy whenever a single bit of digital entropy is transformed to thermal form; however, in principle there is no reason that a digital bit cannot be transformed into as little as 1 bit of thermal entropy.

Even more interestingly, physical entropy can be transformed back into digital form, given sufficiently small and sensitive devices. Imagine a binary device with two metastable states, one more energetic than the other by some small amount, say k_BT ln 2. The device can be initially prepared in the low-energy state, and then allowed to equilibrate with the thermal reservoir by lowering the energy barrier between the states, and then isolated from the reservoir by raising the barrier again. It will be found in the high-energy state half as often as in the low-energy one. Its state is then reversibly measured and copied into a previously-empty bit location. Then, under control of this copy of the state, the device is reversibly restored to the low-energy state, recovering the k_BT ln 2 energy if the device was in the high-energy state. The process is then repeated, generating on each step an average of 0.92 bits of digital entropy (assuming the data is compressed) and removing 1/3 bit of thermal entropy (and the corresponding energy) from the environment, for an entropic efficiency of about 36% (this is the percentage of the entropy in the digital entropy stream that came out of the environment). So, we have taken heat---energy with thermal entropy---and separated it into work, and a somewhat larger amount of digital entropy. The efficiency of the process can approach 100% as we increase the energy difference between the two states of the device, but at a cost of decreasing the average amount of entropy that is removed from the thermal system per step.

Whether in thermal or digital form, entropy is annoying because, once it is created, it permanently takes up space that could otherwise be used for storing useful information. As entropy is generated within a system, if we cannot move it away quickly enough, from a small region of the system in which it is being generated outward to another part of the system where there is more room to store it, then eventually the accumulating entropy will overflow the density with which it can be harmlessly stored, and it will begin to mix with and corrupt the state information of some part of the system whose state we care about---for example, by melting its structure.

Thus entropy generation is a fundamental factor affecting the performance of those computational systems that produce it, as we will show in detail in the next section.

4. Bounds for Irreversible Computation

In this section we derive lower bounds on the time required to perform a certain class of computations on any computer that requires a net increase in information with each operation, such as a computer based on irreversible logic devices that constantly generate new entropy.

The class of computations of interest will be simulations of N×N×N 3-dimensional arrays of elements, each of which has some fixed amount of state information which needs to be updated according to some fixed rule on each step of the simulation. This class of computations is very common and useful for simulating physical systems, such as weather patterns, fluid flow, chemical interactions, particle interactions, stress in structures, and other things. Such computations might also be very useful for simulating nanomechanical systems.

We wish to look at how the speed of the simulation scales as N increases, in various situations. We assume as in §2.3 that information density is limited to a constant 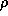. We will allow the number of processing elements in the computer to also scale up as much desired, and we look at what is the maximum speed that can be achieved given any number of processors. This gives a conservative upper bound on what speeds might actually be attainable (and also fits in well with the projections from nanotechnologists that someday manufacturing will be very cheap).

First, let us note that if there is no limit to how far the processing elements can be spread apart, then the entire N×N×N system can be simulated in only O(1) time per step, because we can simply use N³ processors spread out over a large enough area so that entropy removal through the enclosing surface is not a limiting factor. If the job of each processor is just to do some independent task such as searching some part of a large search space, then this sort of architecture can be practical. Witness the projects to do big computations such as factoring large numbers in distributed fashion over the Internet.

However, we were intending to examine a class of computations corresponding to 3-D physical simulations. In such simulations, elements usually need to continuously interact with their immediate neighbors in the array. Cellular automaton simulations of physical systems (Toffoli and Margolus 1987) have this property. In these systems, processing elements can not be spread indefinitely far apart, because then communication delays will increase the time required to perform each update. Let us examine how the constraints of communication time and entropy removal combine to determine the maximum rate for an irreversible simulation.

Even with local interactions only, in simulating the entire space for N steps, each element will in general affect order N³ others for order N steps each, for order N⁴ total element updates that depend on the first element's value.

But in an amount of real time t, the localized datum representing an element's state at the start of that interval can only possibly affect a region of real space of at most radius tc, which can be enclosed in a surface of area order t². From the arguments in §2.3, only a rate of operation of order t² can be sustained in such a region, if each operation produces some constant net amount of information. This gives us a maximum total number of order t³ operations that can depend on the datum in time t. Thus, performing the order N⁴ dependent operations required for N simulation steps requires at least a real time t of order N^4/3, for an average of N^1/3 time per step.

This lower bound can actually be achieved, using for example an array of N×N×N processors spaced a distance of order N^1/3 apart from each other, each performing an update every order N^1/3 time units, which permits enough time for round-trip communication between neighboring processors on each step. A single row of N processors running through this computer produces entropy at a total rate of order N^2/3, and the surface area available for removal of the entropy at the end of this row is also N^2/3, so there is no difficulty in removing the entropy. A more volume-efficient variant of this architecture folds up each row of N processors to fit into an N^1/3×N^1/3×N^1/3 cube, and then the N² cubes are arranged in a flat square array, each cube beside the ones for the neighboring rows.

In the next section we will see that an asymptotically reversible technology can do better, and perform such simulations, at least in some cases, in only order N^1/4 time per step, that is, faster by a factor of N^1/12. This is not so impressive, but allowing processing elements to be spread out over such a large area may be overly generous; after all, real estate is expensive, and wide, flat things are harder to move around than small compact things. So it might be reasonable to impose some additional limits on the growth rate of the computer's diameter. For instance, we might want to specify that the diameter of the computer should not grow faster than order N, i.e., no faster than the logical diameter of the system we're simulating. This rules out the computers above, whose diameters grow as N^4/3.

For order N diameter machines, the surface area grows as order N², which bounds the maximum irreversible processing rate within, so performing the N³ operations required for a simulation step takes at least order N time per step. This bound can be achieved by arranging the processors in a 3-D array packed as densely as possible and running each processor at order 1/N speed.

In the next section we will see that in the constrained-diameter case, reversible machines can run at only order N^1/2 time per step, that is, a factor of order N^1/2 times faster than any irreversible machine.

5. Bounds for Asymptotically Reversible Computation

In the previous section we showed that computers that generate some constant net amount of new information per operation, such as all computers based on irreversible logic devices, cannot perform N×N×N array simulations faster than order N^1/3 time per step, or faster than order N time per step if the machine's diameter is limited to order N. In this section we discuss how asymptotically reversible logic devices can be arranged in parallel architectures that improve on these bounds.

5.1. Asymptotically reversible devices. In the next section we will examine in detail a variety of existing and proposed technologies for digital logic devices which all share the property of asymptotic reversibility. This means that although their operation does produce some new entropy, at sufficiently low speeds the amount of entropy produced scales down as the speed of operation is decreased, with no known unavoidable lower bound. We write:



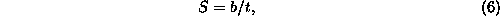
where S is the amount of new physical entropy generated per operation by the device, t is the length of time over which the operation is performed, and b is a constant factor which we hereby call the entropy coefficient or ``badness,'' a characteristic of the device technology in question. Badness has units of entropy times time, or entropy divided by frequency, and simply expresses how much entropy the device generates per operation, per unit of speed at which the device is run. Example units for b: bits per Hertz.

5.2. The case for reversible high-level models. Most current models of computation are based on irreversible primitive operations. For example, in ordinary microprocessor instruction sets, there are many instructions that specify that certain information (such as the previous contents of a register) should be discarded when the operation is performed. Certainly, if such instructions are executed by dissipating the stored information to heat, there is an accompanying production of entropy, and the rate of computation is bounded as we discussed in §4.

Given reversible logic devices, one might try to get around the problem by performing a reversible simulation of the irreversible computation specified by the traditional programming model, as in the linear-time simulation of Bennett (1973). However, when all the physical costs are taken into account, such an approach may not be very efficient. Bennett's linear-time simulation generates information continuously during the first half of the simulation. The information produced is un-derived during the second half, so it is not entropy, but it still must be stored somewhere in the meantime. A computation that needs to run for t time steps thus requires an order t volume of physical space per processor, so we are performing instructions at an order t slower rate per unit volume than if only a constant O(1) amount of space were assigned to each processor.

A later simulation technique by Bennett (1989) uses more reasonable amounts of space, but runs asymptotically slower by a polynomial factor, taking O(t ^{1 + epsilon}) time to execute t steps. The epsilon quantity can approach zero, but only at the cost of exponentially increasing the space usage (Levine 1990). When the space usage is most reasonable, the running time is order t^1.58, and a computation that would take 1 minute to complete on a 100 MIPS processor would take about a year to simulate on a comparable processor reversibly, using that algorithm.

Interestingly, Lange et al. (1997) showed that irreversible computations can be simulated reversibly using no extra space, but their simulation algorithm is too time-inefficient (incurring a worst-case exponential slowdown) to be generally useful.

Is it perhaps possible that arbitrary irreversible computations can somehow be simulated reversibly using both only linear time, like Bennett's (1973) algorithm, and also simultaneously only linear space, like Lange et al.'s (1997) algorithm? Rigorously speaking, that possibility has not yet been eliminated, but it seems very unlikely. Recently our group proved (Frank and Ammer 1997) that if any such simulation technique does exist, then it cannot work in a totally general way that applies independently of whatever arbitrary primitive operations the machine model being simulated might provide.

If we wish to move beyond the limits that irreversible processor architectures apparently place on the space-time efficiency of computation, we must consider the possibility of reversible architectures. Some early reversible processor designs were proposed by Barton (1978), Ressler (1981) and Hall (1994b). Our group is currently designing a reversible processor based on a modern RISC architecture (Vieri 1995, 1996, Frank 1997).

To improve the asymptotics, it is not enough for individual instructions to be reversible; it must also be possible to organize instructions into high-level constructs such as loops and conditionals without necessarily continuously generating new information. And if the machine is programmed in a high level language, that high-level language must itself be capable of expressing user programs that can be compiled to code that does not need to continuously accumulate unwanted information. We are designing a C-like high-level language that supports continuous reversible execution with no net generation of information (Frank 1997b).

To take advantage of such a language, programmers need to write algorithms that avoid generating any more leftover information than is necessary. For example, we have tested our programming language successfully with a program that runs a simulation of the evolution of an electron wavefunction according to the Schrödinger wave equation (Frank 1997b, §5). The program runs indefinitely on a simulation of our reversible CPU at a constant speed per simulation step, and without any net accumulation of unwanted information. In general, simulations of reversible physical systems can be performed in an entirely reversible way without slowdowns; see (Toffoli and Margolus 1987, Margolus 1988) for examples.

For computations other than direct simulations of reversible systems, we do not yet know for certain that the use of asymptotically reversible logic devices can improve asymptotic performance beyond that which can be achieved using irreversible logic. For many problems, the asymptotically fastest algorithms may essentially be two-dimensional algorithms that just constantly produce entropy which is removed along the third dimension. The overheads in additional temporary space and processing needed in order to avoid producing entropy may often outweigh the benefits of being able to perform more primitive operations per second within a given region of space. However, we know of no general results on this issue so far.

However, in §6 we go ahead and propose an architecture based on reversible devices, which we claim ought to be able to directly execute any present or future digital physical algorithm for any problem, without asymptotic slowdowns (except for the case of quantum algorithms). So whatever the most efficient physically-realizable algorithm for a problem turns out to be, whether reversible or irreversible in nature, our architecture ought to be able to efficiently run it. Thus we can postpone the question of finding the most efficient reversible algorithms, and make progress by showing that our reversible architecture is optimal, and is strictly faster than irreversible machines on, at least, one important class of computations, namely 3-D array-based simulations of reversible systems.

5.3. Analysis of reversible asymptotic performance.

First, note that if the entropy produced per operation could be made exactly zero while still having the operation take only some constant amount of time, we could perform our class of 3-D simulations in O(1) time per step by just using a 3-D array of processors assigned to corresponding elements in the N×N×N simulation space, and running them at some constant speed. However, we cannot hope for a device that produces exactly zero entropy per step, independent of speed.

If the entropy generated by a reversible device per operation is instead S = b/t as above, and the device is operated once every t time units (at frequency f = 1/t), then the rate at which entropy is generated by that device per unit time is bf². If there are n reversible devices operating at that frequency in a computer at any given time, then the total rate of entropy generation in the computer is just R = nbf². Solving this for f, we have



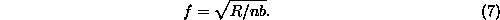
To see how the rate of processing scales with a machine's diameter d, let us observe that the number of active devices n in the machine's volume can scale in proportion to d³, where is the max device density per unit volume, and the total rate of entropy removal through the convex hull can scale as d²F, where F is the entropy flux per unit area. So in terms of d, the frequency f of operation can scale as



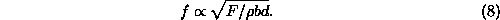
and so the total rate r = nf of operation for the whole computer scales as



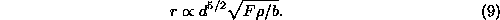
This is better than the irreversible case where the total rate only scaled up with the enclosing area d². Note also that in the reversible case, the maximum speed of a machine of a given diameter increases as the entropy coefficient or volume of its devices goes down. For an irreversible machine, neither of these quantities affects the ultimate speed limits for a machine of a given diameter and rate of entropy removal, because each operation produces constant entropy at least equal to the amount of information that is discarded by the operation.

Now let us derive a lower bound on the time per step when performing our 3-D simulation on an asymptotically reversible machine. As in §4, in time t a datum can only affect a volume of radius order t. The number of processors n in this volume scales as t³, and the allowed rate R = FA of entropy generation within it scales as t² like before, so the processing rate r scales as t^5/2, and the amount of dependent processing in time t scales as t^7/2, so it takes at least order N^8/7 time to do the order N⁴ operations that depend on a datum during N simulation steps, so the average time per simulation step cannot be lower than order N^1/7.

This is only a lower bound; we do not yet know whether it can actually be achieved by any physically possible algorithm. However, we do know that a time of order N^1/4 per step can be achieved, which is still better than the order N^1/3 lower bound for the irreversible case. We do this by using a 3-D array of N×N×N processors spaced a distance of order N^1/4 apart and taking order N^1/4 time per step. The rate of entropy production per processor is then N^-1/2 and the rate for N processors in a row is N^1/2, as is the surface area at the end of the row.

If the diameter of the machine is limited to O(N), then the maximum processing rate r for the whole machine is order N^5/2, so performing the N³ operations required for one simulation step takes at least time N^1/2. This bound can be achieved by a 3-D array architecture; a row of N asymptotically reversible processors each running at frequency N^-1/2 produces entropy at a constant rate.

6. A Proposed Ultimate Architecture

In the previous sections we have sketched out why reversible 3-D parallel machines can be faster than any possible irreversible machine, at least for certain kinds of computations. Now in this section we flesh out the structure of this interesting class of reversible machine architectures in a little more detail, and argue that as we have described them, this class of machines ought to be just as efficient as any other physically possible architecture, within a reasonable constant factor that is dependent on the particular device technology being used, but not on the scale (number of processing elements) at which we are working.

The inspiration for why such a ``universal'' architecture ought to be possible comes from the observation that any computer architecture must ultimately be embedded in the real world, implemented on top of the underlying substrate of physics, and thus can be no more computationally powerful than that substrate. If we can just find an architecture that directly provides a window on all the information-processing capabilities of physics that might be exploited in a computer, and passes those capabilities straight through to the programmer, without adding any fundamental new inefficiencies, then such an architecture ought to be able to perform any general class of computational task without being significantly slower at it than any other possible machine. We will accept constant-factor slowdowns, since no general-purpose machine except physics itself is going to be as fast as any other physical machine even on problems for which that other machine is specialized. But we will not tolerate any architecture that becomes unboundedly slower than some other physical class of machines as problem sizes increase.

The question of designing a real-world computer architecture is largely a question of what to do with available space---what kinds of components to put in it, how to arrange them, how information should move around the space, and so forth. So let us start by considering what are the different possible uses to which a small region of physical space can be put.

Our piece of space can contain information, but as we saw earlier, not more than a certain amount of information, if we wish to maintain reasonable temperatures and energy densities. It can propagate information through itself, though not faster than the speed of light. It can perform reversible interactions between pieces of information, but only locally between nearby pieces of information, and only at a finite rate. New structures of information can be derived from old ones, or can be underived and disappear. In general, because no physical system is perfectly free of unwanted interactions, at any time some small amount of the information in our region of space may go ``off course,'' so to speak, and become entropy that will never be underived.

Another kind of information processing that can occur in a piece of space is that we can form a quantum superposition of a number of different mutually exclusive states, which evolve independently until their paths converge again, at which point they may interfere with each other, producing a different distribution of resulting states than would have occurred if only a single path of evolution had been followed. Taking advantage of interference effects between complex states evolved over long histories is the basic idea behind quantum computation, which, if it can be carried out successfully, appears to be able to perform some kinds of computations asymptotically faster than would otherwise be possible (Shor 1994, Boghosian and Taylor 1997). However, since the implementability and stability of quantum computing at reasonable scales is currently still undemonstrated, we will leave this capability out of our models for now; however, if quantum computing turns out to be practical at some later date, our ultimate model should certainly be extended to include it.

But as for the other capabilities and limitations mentioned above, we should certainly include them in our model. In order for our computer to be asymptotically as efficient as the physics, we want the amount of each capability that is present in a given region of our computer to scale up at the same rate that it does in the physics. This means that each unit of space in our computer, at some fixed scale, should contain at least some constant amount of storage capacity, some constant bandwidth (information flux capacity) through it, and some constant amount of machinery for information interaction. This much is standard in mesh architectures.

However, as we have discovered in the previous sections, it is also important to consider the issue of the rate of the production of entropy, and how it scales in relation to the speed with which interactions between pieces of information take place. If the devices in our processing units are only of the irreversible kind, then the entropy generated when an interaction occurs is fixed, and cannot decrease beyond a certain point. We saw that this leads to asymptotically slower performance than in architectures that provide the ability to use only asymptotically reversible logic devices. Therefore, the processing units in our ultimate computer models should provide such devices.

We surmise that there is no way to implement digital devices that operate at non-infinitesimal speed with exactly zero entropy production per operation, and that, at best, all logic devices will have an entropy per operation that scales in proportion to speed, like the devices we know about.

We can imagine some other capabilities that might be important. One is for the rate of production of entropy per operation to be different in different parts of the computer. It is conceivable that the optimal algorithms for some problems might involve higher rates of entropy production near the edges of the computer, but lower rates in the interior, because entropy produced in the interior would have to travel farther to get out.

Another capability that might be important is to be able to transmit information and entropy perfectly ballistically and at the speed of light. Light or matter can travel through a vacuum with essentially zero attenuation. It seems reasonable to include this capability in the model as well, rather than requiring all information to be moved from one location to another via some active process that either operates slowly or produces significant new entropy at each step. Even entropy can probably be removed ballistically, perhaps by digitizing it and transmitting it out as a dense stream of photons, or perhaps by heating up a material (e.g., a solid ring or a stream of solid pellets or liquid droplets) that is nearly-ballistically moving through the system, say in evacuated tubes.

One other capability that might conceivably be useful is diffusive, random-walk transportation of information such as occurs in chemical systems. This mechanism is interesting because provides a way that information can be communicated between different places without any new entropy being produced along the way. For example, molecules in biological systems often automatically propagate about through a cell via Brownian motion. We could provide this capability by reserving some of the space in each processing unit to contain a fluid through which different kinds of molecules are allowed to diffuse to carry encoded information around the computer. However, it is not yet clear that there are algorithms that would actually be made asymptotically any faster using this kind of transport mechanism than they be if they only used more deliberate mechanisms. It is conceivable that actively routing the information from one place to another would be slower, if it involved entropy generation at each step. But for now, we will consider the chemical network to be an optional addition the the architecture.

That sums up the basic set of capabilities that we anticipate the processing units of our architecture might require. Powering the system is not a significant additional concern, since new free energy only needs to come in to any part of the system at exactly the same rate that entropy-carrying energy is coming out of it, and we have already provided for the entropy flow; fresh energy (work) can just follow along this flow in the opposite direction. Energy can be moved around internally within the system using the same mechanisms that ballistically transmit information. (Of course, we had better have mechanisms for transmitting and receiving work and information that are capable of operating asymptotically reversibly, if this is possible.)

The architecture would be scaled in this model by simply changing the number of fixed-size processing units that are present in the machine.

Of course, a set of capabilities is not a complete design, but we feel that there is a very wide range of reasonable designs that could provide all the basic capabilities as outlined above, and there is no need to try to standardize on a particular one at this early stage. Just about any reversible uniprocessor CPU architecture that has been proposed could be a suitable realization of the model, if implemented in an asymptotically reversible device technology, and augmented with asymptotically reversible and near-ballistic mechanisms for transmitting energy and information between neighboring processors, and also with some coolant material that flows near-ballistically through the system along evacuated tubes, to carry entropy out of the system.

This sort of architecture provides all the basic information-processing capabilities of physics that we can think of (except for quantum coherent operation) and provides them in quantities that scale in the same way as the raw physics. We have made only the reasonable assumption that the laws of physics as currently understood are correct, and also that energy densities in any architecture are limited, so that we do not have to think about packing unbounded amounts of entropy into finite space, or processing information at unboundedly high rates.

We hereby submit to the academic community for evaluation our thesis that, subject to the above assumptions, no physically realizable class of mechanisms can perform any digital computational process strictly asymptotically faster (by more than a constant factor) than the above-outlined class of architectures. This conjecture might be termed ``the tight Church's thesis,'' since it is a more close-fitting analogue of Church's thesis, which conjectures that Turing machines are universal, that is, capable of computing any physically computable function. Our conjecture is also stronger than the so-called ``strong Church's thesis'' of traditional complexity theory, which hypothesizes that Turing machines are at most polynomially slower than any physically-realizable computing mechanism. We conjecture that our class of models is not only computation-universal within a polynomial factor, but is ``ultimate,'' in that it can perform any class of computation exactly as fast asymptotically (within a constant factor) as is physically possible.

Again, the current form of this conjecture is ignoring the possibility of quantum coherent operation, but this can be added to the model later if needed.

7. Performance of Various Technologies

So far in this paper we have mostly just talked about asymptotic scaling behavior of various models, correct only to within constant factors, and we have not talked much about real numbers, or about how large the constants are.

In this section we finally work through the numbers, and determine, for different irreversible and reversible technologies, about how fast they really are, and how they compare to each other at various scales. We will make a variety of different approximations and simplifying assumptions, but we expect that our answers will still be more or less correct, to within about an order of magnitude.

The answers we get will depend on the maximum entropy flux F that can be attained using various technologies for entropy removal (cooling).

7.1. Cooling technologies. Ordinary CPU chips in most present-day computers rarely can dissipate more than 100 W of heat from a square centimeter of chip surface using normal passive cooling mechanisms, such as conduction through a ceramic package and convection through air. The chip surface is normally at least at room temperature (300 K), so the entropy flux attained by these mechanisms is no larger than F = 100 W / (k_B (300 K) ln(2) / bit) = 3.5 × 10²² bit / s cm².

Drexler (1992), §11.5.3, p. 332, has designed a convective cooling system using fractal plumbing that ought to be able to remove at least 10 kW/cm² of heat at 273 K from a surface up to 1 cm thick. This corresponds to an entropy removal rate of 3.8 × 10²⁴ bit / s cm².

If entropy is encoded in some material at the atomic scale at a density 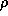of no more than 1 bit per cubic Ångstrom (about an atom-sized volume), and the material moves nearly-ballistically through the computer at no more than v = 1 m/s, the maximum entropy flux F = 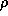v is 10²⁶ bit / s cm². (Allowing most of the machine's volume to be occupied by the cooling material.)

If the material instead moves at a tenth of the speed of light (so relativistic effects are still small), then the maximum flux is 3 × 10³³ bit / s cm².

For materials at the density of water, 1 g/cm³, Bekenstein's fundamental quantum-mechanical bound on entropy (Bekenstein 1984) implies that even if all the material's mass-energy is used for storing information at maximum efficiency, no more than about 1.7 × 10⁶ bits can exist in a region 1 Å across. At a tenth the speed of light this gives a max entropy flux of 5 × 10⁴⁰ bit / s cm².

If entropy is removed digitally through 1 mm-wide 100 GHz optical fiber available today, the maximum flux is only about 10¹³ bits / s cm². The maximum flux that can be achieved using electromagnetic radiation in more efficient optical technologies is unclear, but we should note that the entropy density S/V in a thermal photon gas scales in proportion to T³ (Joos and Qadir 1992, p.571), so it seems that achieving unboundedly high entropy densities in a stream of photons would require unboundedly high temperatures, which we may reasonably disallow.

We should note that the limit on entropy density given by Bekenstein's bound actually increases as information is encoded across regions of larger diameters. If some technology can take advantage of this, then it may change the entire form of the scaling analysis in this paper. However, Bekenstein's bound may not actually be achievable, so for now we will stick with our assumption that for any particular technology, entropy density is finite.

The following table summarizes the above figures.

7.2. Irreversible technologies. In §2.5 we already calculated that the best present CMOS irreversible device technology generates at least 10⁶ bits of entropy per device-switching operation. This number will decrease somewhat over time, as power supply voltages and circuit node capacitances decrease. However, voltages cannot decrease too much because of difficulties in setting threshold voltages accurately, and because of problems with leakage currents, although the latter problem can be addressed somewhat my operating at low temperatures.

One very interesting low-temperature technology is the Rapid Single Flux Quantum (RSFQ) superconducting logic family being developed by Likharev and his colleagues at SUNY (Likharev 1996). This technology may be able to dissipate as little as 10^-18 J of energy per irreversible bit operation at 5 K, which corresponds to an entropy generation of only 21 kilobits.

Finally, we would like to consider a ``best possible'' irreversible technology that produces only 1 bit of physical entropy for each bit of information that is discarded. Merkle and Drexler (1996) argue that their proposed ``helical logic'' electrical logic technology could perform irreversible bit erasure with an energy dissipation approaching kT ln 2, which would create just 1 bit of entropy. Drexler's rod logic is also estimated to be capable of performing close to this limit as well (Drexler 1992, §12.4.3, p. 359). It is expected that as computational devices approach the nano-scale, a wide variety of different device designs will be capable of asymptotically approaching the minimum entropy generation of 1 bit per bit that is irreversibly erased.

In the following table, we calculate the maximum rate of irreversible bit operations per second, per unit of enclosing surface area, for some different combinations of irreversible device technologies and cooling technologies.

7.3. Reversible technologies. We now examine the entropy coefficients of a variety of reversible device technologies. Recall that the entropy coefficient of a technology expresses the amount of entropy generated per device operation per unit of frequency at which the device is operated.

First, current commercially-available VLSI fabrication processes, with ordinary CMOS transistors, can be used to create asymptotically reversible electronic computers. This is done by use of so-called adiabatic switching principles (see for example Athas et al. 1994). In adiabatic circuits, the order CV² energy dissipation of normal circuits is avoided by never turning on a transistor when there is a voltage difference across it. Instead, circuit nodes are always charged and discharged gradually using a resonant power supply that asymptotically recovers all of the energy.

In our group we are building processor chips that operate fully adiabatically, using the SCRL pipelineable reversible circuit style developed by members of our group (Younis and Knight 1994, Younis 1994).

We calculate an entropy coefficient for typical SCRL logic gates fabricated in a fairly recent 0.5 µm VLSI process (HP14) and operating at room temperature of about 43 bits/kHz. In a best available process with around 10 kilohm transistor on-resistance, 1 V power supply, and 60 fF node capacitance, we would have a somewhat lower value of ~6 bits per kHz.

SCRL performance might be even better in an implementation based on low-resistance microelectromechanical switches, as discussed in Younis 1994, §2.7.3, p. 34. However we currently have no figures for the exact resistance and other characteristics of such switches.

Merkle (1993a), p. 35, analyzes the energy dissipation of the reversible transfer of a packet of 100 electrons through a minimal quantum FET, and finds it is around 3×10^-21 J at a rate of 1 GHz. The corresponding entropy coefficient at room temperature is about 1.2 bits/GHz.

Drexler's rod logic, operated reversibly, dissipates about 2×10^-21 J per operation at a speed of 10 GHz (Drexler 1992, p. 354). Its entropy coefficient at room temperature comes out to .070 bits/GHz.

The ``parametric quantron'' superconducting reversible device of Likharev (1982) dissipates about 10^-24 J during a 1 ns operation at around 4 K (p.322); its entropy coefficient thus comes out about .026 bits/GHz.

Finally, Merkle and Drexler's (1996) proposed helical logic was analyzed by them to dissipate around 10^-27 J at 10 GHz and 1 K; its entropy coefficient thus comes out to be 10^-5 bits/GHz.

The following table summarizes these calculations.

Armed with the above figures, we are now in a position to calculate the scale at which the various reversible technologies will beat the various irreversible technologies. We will measure this scale first in terms of the number of devices required per unit area, then for technologies for which we know the device volume, this can be converted to find the diameter (thickness) of the machine.

Based on the analysis of section 5.3, we can express the number of reversible devices N_A per unit area required to achieve a given rate R_A of operations per unit area as

To achieve the same rate of operation achievable by an irreversible machine that produces S bits of entropy per operation and uses the same cooling system, the number becomes

The following table shows the number of reversible devices in various technologies needed to beat the maximum per-area processing rate the 3 combinations of irreversible technologies and cooling technologies down the diagonal of table 2.

The parenthesized numbers indicate cases in which the number of devices required may be determined by the maximum rate of operation of the devices, rather than by the entropy limits. The number given is what the number of devices required would be if the individual devices could run with as high a frequency as needed. The actual number required will most likely be higher.

To make sense of the other numbers in table 4, we estimate the volumes of the logic devices in various technologies. SCRL devices we will take to be about 10 µm × 10 µm × 1 µm = 100 µm³. The quantum FET we estimate at about (10 nm)³, a rod logic interlock as 40 nm³ (Drexler 1992, §12.4.2, p.357), and a helical logic switch as 10⁷ nm³ (Merkle and Drexler 1996, §5.2, p.330)

The parenthesized numbers in this table need explanation. The entries that say "any" indicate that even if the given reversible devices are scattered over a surface in only a single layer, they will still be faster than any machine built with the given irreversible technology within that surface. The 0.1 mm calculated for 10¹² helical logic devices per square centimeter beating the best possible irreversible technology given a 10²⁶ bit/cm² entropy flux, is probably inaccurate because the individual helical logic devices probably couldn't run at the required 100 THz.

The entry in the upper right corner of the table indicates that a machine built with current CMOS reversible technology would have to be the size of the inner solar system before it would be faster than the most efficient possible irreversible technology. Needless to say, a machine this large, composed of solid silicon, would collapse under its own gravity.

In any case, the table indicates overall that most of the listed reversible technologies outperform most irreversible technologies, in terms of raw numbers of operations per second per unit area, for a wide range of cooling capabilities and for machines at a reasonable scale. Current CMOS reversible technology does not perform so well against the most efficient conceivable irreversible technologies, but it can still beat machines based on contemporary irreversible CMOS technology at reasonable scales.

One caveat to the above results is that in general a reversible device operation is not as computationally useful as an irreversible operation, due to the algorithmic issues discussed in §5.2. However, for problems that have efficient reversible algorithms, like the physical simulations that we discussed, a small constant number of reversible device operations should suffice to do as much useful computational work as a single irreversible operation. The diameters in table 5 should be increased by a factor of the same small constant.

8. Conclusion

In this paper we have considered the impact of the laws of physics on the nature of the optimal computer architecture, focusing on the issue of entropy removal, and how it can be partially circumvented by the use of reversible architectures. We determined that computers based on reversible logic devices are indeed asymptotically more efficient than irreversible machines on at least a certain large and interesting class of computations, namely simulations of reversible 3-D physical systems. We outlined a general class of scalable reversible architectures, and conjectured a "tight Church's thesis" that these models represent the most efficient physically implementable architecture, capable of simulating any other physically-implemented computer (apart from quantum computers) with at most constant factor slowdown. Finally, we performed some calculations to compare the raw performance of a variety of reversible and irreversible logic technologies, including both conventional CMOS technologies and molecular nanotechnologies, and found that when the primary constant factors are taken into account, the reversible technologies do indeed turn out to be faster than comparable irreversible ones at all scales above a certain reasonable level.

Given the apparent asymptotic superiority and universality of reversible 3-D architectures, we suggest that computer scientists begin studying this class of models in earnest, developing good parallel algorithms for them, and that computer designers begin developing convenient and powerful programming models for them. If we are correct that this class of architectures is asymptotically optimal, then work we do now on algorithms and programming models for the architecture will never become obsolete. This contrasts with the typical existing parallel algorithms and programming models, which ignore important physical constraints, and therefore may not scale as well as possible, as technology improves and machines become more highly parallelized.

We can infer from our results of the previous section that already, in current CMOS technology, a stack of only on the order of 200 layers of reversible circuitry would be able to perform more operations per second per unit area than any possible machine composed of conventional irreversible circuits built using the same VLSI fabrication process. This quite reasonable number suggests that a well-designed reversible machine could have commercial value today, at least for performing computations such as large-scale 3-dimensional physical simulations.

Moreover, as better device technologies become available, the advantages of reversible architectures will only increase. As computing technology continues to approach the nano-scale, a sophisticated understanding of reversibility and other fundamental issues in the physics of computation will be essential for the creation of the most powerful nano-supercomputers of the coming century.

Acknowledgments

Thanks to Norm Margolus, co-author of the UMC-98 paper (Frank et al. 1997) from which this paper is largely derived, for his ongoing intellectual guidance and many helpful discussions.

This work was supported by DARPA contract DABT63-95-C-0130.

References

Athas, W.C; Svensson, L.``J.''; Koller, J.G.; Tzartzanis, N.; and Chou, E.Y.-C. (1994)

IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2(4). Low-Power Digital Systems Based on Adiabatic-Switching Principles. See also http://www.isi.edu/acmos/acmosPapers.html

Barton, E. (1978)

MIT term paper. A Reversible Computer Using Conservative Logic

Bekenstein, J.D. (1984)

Physical Review D 30(8), pages 1669-1679. Entropy content and information flow in systems with limited energy

Bennett, C.H. (1973)

IBM J. Research and Development 17(6), pages 525-532. Logical reversibility of computation

Bennett, C.H. (1989)

SIAM J. on Computing 18(4), pages 766-776. Time/Space Trade-offs for Reversible Computation

Bilardi, G. and Preparata, F. (1993)

Technical report CS-93-20, Brown University. Horizons of parallel computation

Boghosian, B.M. and Taylor, W., IV (1997)

http://xxx.lanl.gov/abs/quant-ph/9701019. Simulating Quantum Mechanics on a Quantum Computer.

Drexler, K.E. (1992)

John Wiley & Sons, Inc. Nanosystems: Molecular Machinery, Manufacturing, and Computation

Englert, F. (1997)

http://xxx.lanl.gov/abs/hep-th?9705115. On the black hole unitarity issue

Frank, M.P. and Ammer, M.J. (1997)

Extended abstract to be submitted to CCC-98. Separations of reversible and irreversible space-time complexity classes

Frank, M.P.; Knight, T.F., Jr.; and Margolus, N.H. (1997)

Paper to be presented at the First International Conference on Unconventional Models of Computation (UMC-98). Reversibility in optimally scalable computer architectures

Frank, M.P. (1997)

MIT Reversible Computing Project Memo #M7. Modifications to PISA architecture to support guaranteed reversibility and other features

Frank, M.P. (1997b)

MIT Reversible Computing Project Memo #M8. The R Programming Language and Compiler

Hall, J.S. (1994)

Nanotechnology 5, pages 157-167. Nanocomputers and reversible logic

Hall, J.S. (1994b)

Proceedings of the Workshop on Physics and Computation: PhysComp '94. IEEE Computer Society Press. A Reversible Instruction Set Architecture and Algorithms

Joos, E. and Qadir, A. (1992)

Il Nuovo Cimento 107B(5), pages 563-572. A quantum statistical upper bound on entropy

Landauer, R. (1961)

IBM J. of Research and Development 5, pages 183-191. Irreversibility and Heat Generation in the Computing Process

Lange, K.-J.; McKenzie, P.; and Tapp, A. (1997)

In proc. 12th Annual IEEE Conf. on Computational Complexity, pages 45-50. Reversible space equals deterministic space

Lecerf, Y. (1963)

Comptes Rendus Hebdomadaires des Seances de L'academie des Sciences 257, pages 2597-2600. Machines de Turing réversibles. Insolubilité récursive en de l'équation 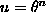, où 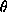est un ``isomorphisme de codes''

Leighton, F.T. (1992)

Morgan Kaufmann. Introduction to Parallel Algorithms and Architectures: Arrays · Trees · Hypercubes

Levine, R.Y. and Sherman, A.T (1990)

SIAM J. on Computing 19(4), pages 673-677. A Note on Bennett's Time-Space Tradeoff for Reversible Computation

Likharev, K.K. (1982)

International Journal of Theoretical Physics 21(3/4), pages 311-326. Classical and Quantum Limitations on Energy Consumption in Computation. See also http://pavel.physics.sunysb.edu/RSFQ/RSFQ.html

Likharev, K.K. (1996)

http://pavel.physics.sunysb.edu/RSFQ/Research/WhatIs/rsfqwte1.html. Rapid Single Flux Quantum (RSFQ) Superconductor Electronics

Likharev, K.K. and Korotkov, A.N. (1996)

Science 273(9 Aug), pages 763-765, ``Single-Electron Parametron'': Reversible Computation in a Discrete-State System

Margolus, N.H. (1988)

MIT PhD Thesis, MIT Laboratory for Computer Science technical report MIT/LCS/TR-415. Physics and computation

Margolus, N.H. and Levitin, L.B. (1996)

T. Toffoli, M. Biafore, and J. Leao, eds., PhysComp96, pages 208-211. The maximum speed of dynamical evolution

Mashkevich, V.S. (1997)

http://xxx.lanl.gov/abs/gr-qc/9707055. Conservative Model of Black Hole and Lifting of the Information Loss Paradox

Merkle, R.C. (1993a)

Nanotechnology 4, pages 21-40. Reversible electronic logic using switches. See also http://nano.xerox.com/nanotech/reversible.html

Merkle, R.C. (1993b)

Nanotechnology 4, pages 114-131. Two types of mechanical reversible logic.

Merkle, R.C. and Drexler, K.E. (1996)

Nanotechnology 7(4), pages 325-339. Helical logic

Preskill, J. (1992)

http://xxx.lanl.gov/abs/hep-th/9209058. Do Black Holes Destroy Information?

Rabaey, J.M. (1996)

Prentice-Hall. Digital Integrated Circuits: A Design Perspective

Ressler, A.L. (1981)

MIT Masters Thesis. The Design of a Conservative Logic Computer and a Graphical Editor Simulator

Shor, P.W. (1994)

Foundations of Computer Science, Proc. 35th Ann. Symp., pages 124-134. IEEE Computer Society Press. Algorithms for Quantum Computation: Discrete Log and Factoring

Toffoli, T. (1977)

J. Computer and System Sciences 15, pages 213-231. Computation and Construction Universality of Reversible Cellular Automata

Toffoli, T. (1980)

MIT Lab for Computer Science technical memo MIT/LCS/TM-151 (out of print; available from NTIS). Reversible Computing

Fredkin, E.F. and Toffoli, T. (1982)

Int'l J. of Theoretical Physics 21(3/4), pages 219-253. Conservative logic

Toffoli, T. and Margolus, M. (1987)

MIT Press. Cellular Automata Machines: A new environment for modeling

Vieri, C. (1995)

MIT Masters Thesis. Pendulum: A Reversible Computer Architecture

Vieri, C. (1996)

MIT Reversible Computing Project internal memo. The Pendulum Instruction Set Architecture (PISA)

Vitányi, P.M.B. (1988)

SIAM J. on Computing 17, pages 659-672. Locality, communication and interconnect length in multicomputers. See also http://www.cwi.nl/~paulv/physics.html

Vitányi, P.M.B. (1995)

Proc. 20th Int. Symp. Mathematical Foundations of Computer Science, vol. 969 of Lecture Notes in Computer Science, Springer-Verlag, pages 106-128. Physics and the New Computation

Younis, S.G. and Knight, Jr., T.F. (1994)

International Workshop on Low Power Design, pages 177-182. Asymptotically Zero Energy Split-Level Charge Recovery Logic

Younis, S.G. (1994)

MIT PhD Thesis. Asymptotically Zero Energy Computing Using Split-Level Charge Recovery Logic.