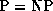Important Open Questions

Other techniques besides the above are known for transforming arbitrary irreversible algorithms into reversible ones, but all known techniques involve prohibitive asymptotic increases in either time complexity, space complexity, or both. However, no one has proven that such inefficiencies are actually required to compute reversibly. Moreover, no one has even thoroughly investigated the question of whether we can compute efficiently if we relax the reversibility constraint a little bit, and merely require that very little information (rather than none at all) be discarded. This suggests several very interesting open questions:

1. Can we prove whether full reversibility actually requires greater asymptotic (ignoring constant factors) space and/or run time on some classes of problems?
2. Can we find and characterize other classes of problems or algorithms in which full reversibility does not decrease efficiency?
3. Can we describe how to reduce the amount of information erasure needed for a computation by arbitrarily large finite factors, without incurring asymptotically decreased efficiency? How quickly does efficiency fall off as erasure decreases?
4. Can we organize and facilitate the programming process so that the theoretical techniques for providing reversibility (to various degrees) can be applied to make it practical to actually write fairly efficient programs for reversible computers?

The first question is extremely difficult, since proving it would involve showing that no reversible algorithm, out of the enormous space of all possible algorithms, could solve a problem with a certain efficiency; this sort of proof has historically been very difficult for complexity theorists to come up with. (Witness the unresolved status of th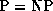e question.) I am sure I cannot do it, but it is an interesting question to raise.

The second question might be more approachable, since I am aware of certain classes of algorithms that can be transformed into a reversible form without increasing either their asymptotic time or space complexity. However, this does not rule out the existence of a better irreversible algorithm for solving the same problem. Still, it would be of interest to know what features of a given algorithm allow it to be made reversible without incurring inefficiency.

I believe the third question can be answered straightforwardly, using a restricted version of Bennett's full-reversibility transformation. Other techniques such as traditional data compression might be used to improve the answer even further.

The fourth question is practical rather than theoretical, and is very straightforward since it is mostly involves just some software engineering design work, rather than proving new and difficult theorems.

These questions can be summed up as a single question: ``Can we make it practical to program computers to compute highly efficiently while requirements for reversibility become more stringent, up to and including the limit of full reversibility?'' This question will be crucially important if we ever wish our computing technology to achieve extremely high computational speeds and densities, without being limited by the need to export to the outside world all the unwanted intermediate results that are generated, in some form such as heat.

The thesis will explore this question, and the various components of it that are listed above.