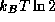Theory of Reversible Computational Complexity

The aim of the theoretical work will be to develop the beginnings of a theoretical study of computational complexity that accounts for reversibility, and measures it by counting the amount of information that is erased during a given procedure (this is zero for a fully-reversible computation). We might call this the ``thermodynamic complexity'' of an algorithm, as opposed to its time or space complexity. Because of the 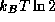energy dissipation per bit erased, the thermodynamic complexity of an algorithm is the fundamental measure of the minimum amount of energy required to execute the algorithm.

As is usual with computational complexity, we will characterize thermodynamic complexity in a way that ignores constant factors, since the exact number of bits erased internally during a particular operation are assumed to vary depending on the particular computer architecture being used. However, we will assume that the architecture provides a universal set of reversible computational primitives which all incur a thermodynamic cost of zero, that is, they are implemented in a way that does not erase any bits internally. The Pendulum architecture designed by Carlin Vieri [6] is an example of such an architecture. In fact, Pendulum does not provide any irreversible primitives, and is not meant to be used to program partially-reversible algorithms. In contrast, we will assume an architecture that also provides an ``ERASE'' instruction that erases a fixed-size unit of information at a thermodynamic cost that is bounded by a machine-specific constant. The zero-cost reversible primitives, together with the ERASE instruction, constitute a sufficient language for describing arbitrary algorithms and analyzing their thermodynamic complexity.

My plan for my study of thermodynamic complexity is as follows:

1. For a number of practical and interesting algorithms from traditional computer science (e.g., from [3]), such as algorithms for sorting, searching, and optimization problems, I will determine the algorithms' thermodynamic complexity when they are translated to the form of reversible primitives plus ERASE in the most straightforward way. I expect most of the traditional algorithms will constantly perform irreversible operations, and thus have thermodynamic complexity equal to their time complexity.
2. I will attempt to find ways to modify the existing algorithms in ways that reduce their thermodynamic complexity without increasing their asymptotic time or space complexity, or else increasing it as little as possible.
3. I already know some examples of algorithms that can be transformed into an equally-efficient reversible form. I will describe these algorithms and attempt to characterize more generally what it is about these algorithms that allows this transformation to be done, and apply that characterization to try to translate other algorithms to an efficient reversible form.
4. I will study and describe the existing very general techniques such as Bennett's for translating arbitrary algorithms into a less-efficient but reversible form. I will attempt to improve on these techniques, but I do not anticipate finding a better transformation for achieving total reversibility. However, I will describe variations on these techniques that achieve greater space and run-time efficiency by incurring a non-zero, but small, cost in thermodynamic complexity.

I plan to spend only three months, January through March of 1997, exploring these issues. Some of the theoretical questions I am asking are very difficult, and so I will not expect to be able to answer all of them to my satisfaction. It will be necessary to cut short the time spent on them, in order to avoid the risk of using up all the time available for the thesis on what might be an impossibly difficult task that may produce no new hard results.

However, I expect that even if all I can do is to formalize the questions, and describe particular examples of efficient reversible algorithms, it will still be worth the effort, and may provide important insights necessary for more far-reaching future work.