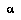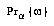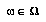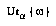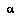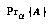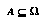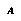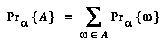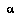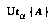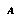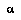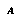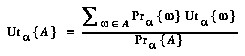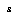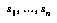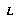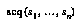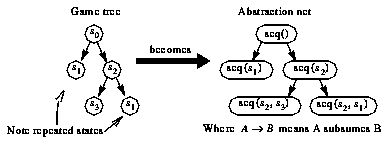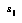Rational abstract search
Michael P. Frank MIT Lab for Computer Science Email: mpf@lcs.mit.edu(1)
Table of Contents
Draft,
Abstract
Computer game-playing (CGP) is potentially a good arena for the investigation of planning techniques. However, most CGP methods developed so far take a very limited view of planning and reasoning. Specifically, they focus on state-space search, to the exclusion of more abstract kinds of reasoning about the future.
In this paper, I motivate the use of abstraction in game-playing, describe various kinds of abstraction that might be useful in game-playing and planning, and show how they can all be subsumed under a unifying definition of abstractions. I propose a methodology for abstraction research that involves translating existing CGP methods into a language of abstraction networks before trying to generalize those methods to work with a variety of types of abstractions. I then summarize the results of my master's thesis work, in progress, on applying decision-theoretic techniques to do effective and efficient reasoning within the abstraction-network framework.
Games, with their well-defined and relatively simple rules, offer a good starting point for the development of AI techniques ultimately intended for general-purpose planning. However, computer game-playing (CGP) research has so far focused mostly on a very narrow range of state-space search techniques, which are only appropriate for a very restricted class of games, and which use reasoning resources inefficiently, even within that class. Many people have recognized that to achieve better generality and efficiency, a more abstract kind of reasoning will be required. In the research-in-progress reported here, I am beginning to work towards the goal of efficiently and effectively reasoning with abstractions for game-playing and other kinds of planning.
In my work so far, I have noted several different kinds of abstractions that have been used, explicitly or implicitly, in existing planning systems and game-playing programs, and I have thought of many more hypothetical kinds of abstractions that might be helpful in game-playing. So as a first step, I describe a simple unifying framework, in which all of these kinds of abstractions can be expressed in the same terms, as abstract descriptions of possible world-histories.
Submitted to the AAAI Fall `93 symposium on Games: Planning, Playing, and Learning.
Available for anonymous FTP from medg.lcs.mit.edu in /pub/mpf/RAS-paper.ps
I then propose that a useful way to begin to understand how to do abstract reasoning would be to translate existing game-playing and planning techniques into the terms of this common framework, so that we can clearly see how abstraction is currently being dealt with by those techniques, and how to generalize the current methods to use abstraction in a more general and flexible way.
I have begun doing this translation for existing game-tree search techniques. I reinterpret game-tree search as exploration of a graph of nodes representing different abstractions, with arcs representing various useful relationships between abstractions. I translate some probabilistic evaluation-function-learning and tree-evaluation techniques into this abstraction-network paradigm. Probabilistic methods were chosen because they are more general, have a clearer semantics, and make fewer assumptions than other methods.
In order to understand the meaning of the translated algorithms, I define a semantics for the "value" of an abstraction, in terms of the expected utility of the event that the actual world-history is described by that abstraction. I also define what it means for an abstraction to have a probability. Armed with these definitions, and with existing game-search techniques translated into abstraction-net terms, I have begun to generalize those techniques to handle additional kinds of abstractions in the abstraction net, and to do more general kinds of search through the net.
I am working on implementing these more general techniques as I develop them. I am currently working in the domain of the solitaire card game "Spider," a relatively simple game in which several kinds of abstraction are needed in order to play the game well.
I anticipate that decision-theoretic search-control techniques, such as those developed for ordinary state-space search by Russell & Wefald [6] and Baum & Smith [1], will be even more important for controlling search in the more complex and flexible space of abstractions. I have a few things to say about how such search control might be done, but many details remain to be worked out.
Section 2 motivates the use of computer game-playing as a stepping-stone towards general planning. Section 3 describes how an over-emphasis on state-spaces leads to the limited nature of current game-playing methods, and motivates the need for abstraction. Section 4 describes several kinds of abstraction that are used implicitly or explicitly in current game-playing and planning techniques. Section 5 defines a unifying concept of abstraction for use in planning and game-playing. Section 6 motivates the translation of existing game-search techniques into this abstract framework. Section 7 defines the meaning of the probability and utility of an abstraction. Section 8 introduces the concept of an abstraction net and diagrams an example. I conclude with a summary of my work-in-progress on abstraction-net algorithms and a description of what I hope to accomplish.
Planning is reasoning about a hypothetical or real future situation that facilitates making an informed recommendation (a plan) about what to do in such a situation, possibly with justifications, for use by some agent (often the same agent that is doing the planning). Planning is necessary because we want our agents to perform well, and since we generally don't have an oracle that can always tell the agent the right thing to do on demand, at some point reasoning must be performed to figure it out. Once a plan has been made, it can serve as a sort of substitute for the non-existent oracle, quickly telling the agent what to do.
Games serve as useful microcosms for testing planning techniques, in lieu of more complex "real-world" domains. The games used in AI research are generally characterized by simple, well-defined rules(2). Such games can still be very rich environments, involving factors like hidden information, chance events, other agents with unknown strategies, and the passage of time. Thus, games offer opportunities for testing solutions to many of the problems that occur in planning in real-world domains.
Unfortunately, the potential of games as a domain for planning remains largely unrealized, because most of the existing work in computer game-playing has made a particular, very strong set of assumptions about what kind of reasoning will be performed by the programs doing the planning. These assumptions restrict the range of games that can be handled appropriately by the reasoning technique, and limit its general applicability towards other kinds of planning. They also, I believe, hurt performance compared to what could ultimately be achieved by more general reasoning methods.
An important characteristic of any approach an agent might take to solving a problem is the ontological stance the agent exhibits towards the problem domain; that is, its idea of the fundamental objects and properties that exist in the domain. Traditionally, computer game-playing researchers have almost always adopted the state-transition ontology for understanding a game. In this ontology, the micro-world of the game occupies some definite state at any time, out of a well-defined state-space; change in the world occurs via well-defined transitions between states.
The state-transition ontology is natural, given that we CGP researchers only intend to address games having well-defined rules, and often, these rules themselves define the game in terms of states and state-transitions (such as an arrangement of pieces on a board, and a set of legal moves). Game designers and players find games based on states and transitions easy to describe and think about. Also, in computer science, we have a natural representation corresponding to states and transitions: the graph, with its nodes and arcs.
However, adopting the state-transition ontology entails many consequences (some perhaps unforeseen) for the kinds of reasoning done by our game-playing programs.
One consequence is that, in our attempt to keep things simple, we tend to think about the state of the world as consisting only of the game-position as discussed in the rules, when other properties of the world may also be important to the task of planning good moves; for example, the passage of real time, the mental states of the players, and the history of past game-positions. As a result, the reasoning techniques we develop tend to neglect those properties, and they end up only being addressed in an ad-hoc way, or not at all.
Additionally, when we focus on states and state-transitions as the fundamental entities, we tend to develop algorithms that work by taking advantage of this simple structure; by traversing the state-graph, examining individual states. As a result, we tend to restrict our attention to the limited class of games in which such exploration is not obviously inappropriate. For example, here are some cases in which state-graph exploration is drastically inappropriate. In each of these, the need is apparent for a less limited, more abstract way of reasoning about the problem:
- A card game with lots of hidden information, where the current state could be any of an astronomical number of possible states. Instead, it might be better to abstract out the hidden information, and focus on the state of the cards we can see.
- A continuous-motion video-game, in which important changes happen only gradually over many dozens of state-transitions. Instead, we might want to abstract over individual ticks, and instead focus on large-scale transitions that involve many atomic actions.
- A war-game with simultaneous motion of dozens of pieces, so that the number of possible transitions (or branching factor) from any state is astronomically large. In this case, it seems necessary to abstract over many of the details of moves being considered, and instead refine a partially-specified plan of action.
I claim that the same kinds of abstractions whose necessity is obvious in the above example are also needed in traditional CGP games like chess, in order to achieve really efficient use of reasoning resources. The need for abstraction in those games has simply been less obvious, because the state-space is barely simple enough so that the amazing speed of our computers is sufficient to allow brute-force state-space methods to work fairly well. But I predict that once abstraction methods have been studied for as long as the brute-force methods have been, abstraction methods will easily beat brute-force methods, even in games like chess, when given the same computational power.
Abstraction in planning and game-playing is not a new idea. In fact, existing game-playing programs use abstraction in several ways. The common notion of game "state" abstracts out the time, the history of previous states, and the mental state of the players.(3) Evaluation functions often work by further abstracting the game-state to a class of states that are the all same along certain "feature" dimensions. A node in a graph of game-states can be viewed as an abstraction of all the possible game-histories in which that particular game-state corresponding to the node is reached.
However, we can imagine a number of additional kinds of abstraction that might be useful as well. We might want to abstract over states, sequences of states, and state-transitions, as suggested in the previous section. We can also draw ideas for kinds of abstraction from research in planning:
- We might want to think about several possible future moves/actions/state-transitions without specifying their chronological order. This kind of abstraction is the basis of nonlinear planning. It can also apply to game-playing: in a situation with many moves available, you might want to consider the possibility "do both (move A) and (move B)," without necessarily deciding, at first, which game-turn you will do the moves on, or even which one you will do first.
- We might want to be able to consider performing some large, high-level action, without specifying, at first, the atomic moves that will be performed in carrying out that action. For example, in chess we might want to think about the general consequences of attacking the opponent's pawn structure, before going to the trouble of figuring out exactly how, where, and when to do it. Such abstraction to high-level actions is the type of abstraction found in abstract planning.
- Very closely related to the above, is planning that works by coming up with relatively easy subgoals that might be useful in attaining our overall objective, and only later figures out exactly how to achieve them, and how to proceed after achieving them. For example, in chess, you might decide it would be good to capture some particular enemy piece, and only then figure out how. This kind of subgoaling is used by island-driven planning.
So given the large variety of kinds of abstraction found both in existing game-playing programs and in planners, it might be worthwhile to spend some time considering what they have in common, and whether a unified view of abstraction might offer some guidance in the quest to make game-playing programs more general and more capable.
At first the various kinds of abstraction we might want in a game-playing program seem very different. Might it be possible to express some of them in terms of others? The first kind of abstraction I mentioned was abstraction over some of the details of a world-state, for example, ignoring the identity of hidden cards in a card game. We can presumably form graphs of such abstract states, and describe possible transitions between them. For example, in a solitaire game, even if many cards are hidden, it may still possible to plan a sequence of several moves, as long as those moves don't depend on the identity of the cards that are still unknown.
But can the other kinds of abstractions be represented in terms of abstract states? For example, consider the nonlinear-planning type of abstraction, in which I consider doing move A and move B but I don't say when or in what order. The only way to coerce this into an abstract state is to have "a state sometime in the future in which move A and move B have been done" as a possible type of abstract state. However, this seems awkward and inelegant.
Instead, I take a different approach. Instead of building upwards from states, adding unnatural properties to them such as information about the history of previous states, I build top-down from abstract descriptions of possible entire histories of the world, adding restrictions to them, similarly to how Wellman defines abstract plans in [8].
Let us imagine there is some space 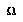 of all the possible complete histories of the world (or of the micro-world of the current game). Then let us define an abstraction
of all the possible complete histories of the world (or of the micro-world of the current game). Then let us define an abstraction 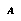 to be a description(4) of a class of world-histories. For any
to be a description(4) of a class of world-histories. For any 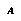 there is some subset
there is some subset 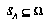 containing the world histories that satisfy the description. An abstraction will generally describe some properties of the world-history, while leaving many others unspecified. Of course, to make this definition concrete we must have some well-defined language
containing the world histories that satisfy the description. An abstraction will generally describe some properties of the world-history, while leaving many others unspecified. Of course, to make this definition concrete we must have some well-defined language 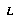 in which we express our abstractions.
in which we express our abstractions.
It is useful to associate with 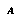 the abstraction-proposition
the abstraction-proposition 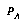 that asserts that the actual world-history will turn out to satisfy
that asserts that the actual world-history will turn out to satisfy 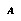 . An agent's belief or disbelief in
. An agent's belief or disbelief in 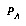 can be an important property of
can be an important property of 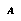 .
.
All of the kinds of abstractions mentioned in section 4 can be subsumed under this definition, as follows:
- A node in a traditional graph of game-positions corresponds to an abstraction of the game-histories in which that game-position is reached.
- Likewise, a node in a traditional game-tree (with repeated states) corresponds to a proposition that the current game will begin with a particular sequence of moves (or game-positions).
- When a game-state is generalized to a class of similar states, for purposes of evaluation, the general class can be identified with a proposition that a game-state is reached that has such-and-such values for various features.
- We can abstract over hidden information or irrelevant details in the game-state with a proposition that a particular abstract (incompletely-specified) state is reached in the current game.
- We can represent abstract (long-term) actions with abstractions of world-histories in which the high-level action is performed.
- We can represent island subgoals with abstractions of world-histories in which the subgoal is achieved.
- We can represent partially-specified moves with propositions that a move satisfying certain conditions is made in the current game.
Moreover, this framework offers the possibility of being less abstract than the standard approach (depending on the language 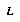 ). A proposition can include statements about the remaining time or about the present or future beliefs and intentions of the players; information that the limited concept of game position is not suited to express.
). A proposition can include statements about the remaining time or about the present or future beliefs and intentions of the players; information that the limited concept of game position is not suited to express.
Having a unifying conceptual framework is all well and good, but we still face the very hard problem of how to actually do effective, efficient reasoning involving abstractions. My methodology for approach this problem has two primary motivations.
The first is the observation that existing game-playing programs and planning systems already do abstraction in several ways, as described above. The hope of my research is that by presenting a unifying definition for abstractions, we can more easily see how to take the existing methods that are being used for reasoning with these specific kinds of abstractions, and translate them to work on other kinds of abstraction as well. For example:
- Game-playing programs explore a partial graph of neighboring states, collect estimated value information at the fringe of the partial graph, and propagate this information back through the graph to make a decision at the root. Could we possibly do something similar for a partial graph of neighboring (closely-related) abstractions?
- Planning systems start with abstract, partial plans and refine them to become more specific, more complete. Can we do similar refinement in this more general framework of abstraction?
The second claim is that, more specifically, methods of probability and decision theory will be needed to interpret information gained by abstract reasoning, and allow efficient search in the relatively large and unconstrained space of abstractions. Decision theory will be needed even more than in regular state-space search, where it is being used already:
- Some game-playing programs (see [1], [4]) fruitfully use probabilistic inference to learn evaluation functions that inductively evaluate states based on past experience with an abstract class of similar states. Can these methods be used more generally, to use past experience with high-level abstractions to draw conclusions about lower-level abstractions that they subsume?
- Many researchers ([1], [5]) have devised ways to treat information gained from a partial game-tree search as probabilistic, and propagate this probabilistic information up the tree. Could we use similar techniques in general to propagate information from more-specific abstractions to less-specific ones that subsume them?
- Some game-playing programs ([1], [7]) successfully apply concepts from decision theory to control exploration of game-trees. Might it be helpful to do decision-theoretic search control in the much larger and more difficult space of abstractions?
Recent work in computer game-playing, such as [1] and [7], has begun to use the decision-theoretic concept of expected utility to define the value of game-states and the usefulness of reasoning actions, and to use probabilities to express uncertainty about the results of future state-space search and about the future decisions that agents will make. Can we use the tools of decision theory in a similar way in reasoning about abstract future-histories, as opposed to specific game-states?
First, what would it mean for an abstraction, a general proposition about the future, to have a utility? If we assign a utility to a proposition about the future, what exactly does that mean, given that we don't know exactly how that abstraction will be instantiated?
There is a very similar problem in the mathematical logic of preference, where the issue is how to define what it means to prefer a proposition's being true to its being false. One approach, taken by Doyle et. al. in [2], is to define preference among propositions in terms of preferences among the possible worlds that satisfy them.
Similarly, we might try to define the utility of a proposition in terms of utilities of possible worlds (or in our case, world-histories) that satisfy it. But how is this to be done? Different worlds satisfying the proposition might have wildly varying utilities, depending on exactly how the proposition is satisfied. For example, the utility of an abstraction in chess, such as capturing the enemy queen, might depend on what I do to achieve it, how much time I take to do it, and what will happen afterwards, all of which might not yet be specified.
A natural answer is that the utility of an abstract proposition is its typical utility if it were satisfied in a way we expect it to be satisfied. For example, I might expect that if I capture the queen I will probably damage my pawn structure in the process, that I will not spend much of my remaining clock time planning the capture, and that afterwards such-and-such other events are likely to occur.
In order to define this "typical" utility, we imagine that worlds have probabilities as well as utilities. Then the utility of an abstract proposition can be defined as the expected utility of the worlds that satisfy it. A side effect is that we can define the probability of the proposition as well.
More formally, let us imagine that at any given time, the agent 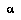 has a subjective probability distribution
has a subjective probability distribution 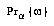 over all the possible future world-histories
over all the possible future world-histories 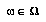 , and a subjective utility
, and a subjective utility 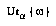 for each of them as well. (This is for definitional purposes only; we don't require that our agents actually could assess probabilities and utilities for every possible world-history, just that the agents can be thought of as implicitly having such probabilities and utilities.)
for each of them as well. (This is for definitional purposes only; we don't require that our agents actually could assess probabilities and utilities for every possible world-history, just that the agents can be thought of as implicitly having such probabilities and utilities.)
Then, I define 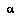 's probability
's probability 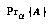 for an abstraction
for an abstraction 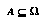 to be the sum of the probabilities of the world-histories in
to be the sum of the probabilities of the world-histories in 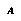 :
:
(EQ 1) 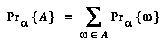
And I define 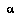 's utility
's utility 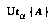 for
for 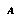 to be
to be 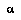 's mathematical expectation of the utility of the world-histories in
's mathematical expectation of the utility of the world-histories in 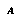 :
:
(EQ 2) 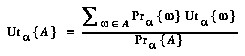 .
.
State-space-oriented game-playing programs generally work by examining a tree or graph of nodes representing game-states, connected by arcs representing legal state transitions. In order to translate state-space search algorithms into abstraction terms, we must first translate game-graphs. We define the translation to be a network of abstractions, connected by arcs representing various kinds of relationships between abstractions, the primary one being a subsumption relationship. Abstraction networks are thus similar to Wellman's plan-specialization graphs [8], except that we allow other kinds of relationships between nodes besides subsumption, and nodes represent abstractions of any aspect of the world-history, not just abstractions over actions performed by the current agent.
As described in §5, a game-state 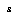 can be interpreted as an abstraction of the world-histories in which that game-state arises. A node in a typical game-tree, however, does not correspond exactly to a game-state, because there may be more than one node for each game-state (unless the concept of game-state is coerced to include the history of previous states). A node in a game-tree is, rather, an abstraction of the histories in which a certain initial subsequence
can be interpreted as an abstraction of the world-histories in which that game-state arises. A node in a typical game-tree, however, does not correspond exactly to a game-state, because there may be more than one node for each game-state (unless the concept of game-state is coerced to include the history of previous states). A node in a game-tree is, rather, an abstraction of the histories in which a certain initial subsequence 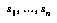 of states follows the current or root state. We presume that this kind of abstraction is describable in our abstraction language
of states follows the current or root state. We presume that this kind of abstraction is describable in our abstraction language 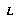 , and we write this abstraction
, and we write this abstraction 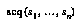 . To complete the translation of game-trees, we need to translate the relation expressed by game-tree arcs into the abstraction framework. The normal parent-child relation in a game tree becomes a subsumption relationship between abstractions. (See figure.)
. To complete the translation of game-trees, we need to translate the relation expressed by game-tree arcs into the abstraction framework. The normal parent-child relation in a game tree becomes a subsumption relationship between abstractions. (See figure.)
FIGURE 1. Translating a game tree into an abstraction network
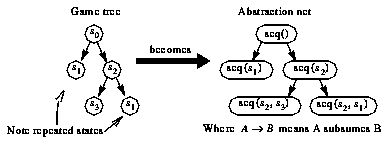
Note that in the abstraction net, the difference between the two occurrences of 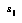 is made explicit, instead of being implicit in the graph structure.(5)
is made explicit, instead of being implicit in the graph structure.(5)
We can also translate game graphs into abstraction nets, for the case of game-playing algorithms that can identify repeated states (with transposition tables, for example). However, space forbids describing this translation here.
Now, having figured out what some existing techniques are doing in abstraction terms, I am working on developing algorithms for correctly propagating probability and utility information through abstraction nets containing arbitrary abstraction nodes connected by subsumption arcs and a few other types of relations. These algorithms are still in flux, so I will not attempt to describe their workings here. However, I will say that the methods I am investigating are partly inspired by the belief-network propagation algorithms described by Pearl in [6], and by Baum and Smith's probabilistic game-tree methods ([1], reviewed in [3]).
In the next few months, I plan to have the propagation algorithms specified well enough to implement them in a program to play the solitaire card game called "spider." Spider is an interesting domain for abstraction because it is a partial-information game where efficient planning requires abstracting over the unknown information. (I decided not to work on a two-player game because it would introduce additional complexities unrelated to the issues I want to study.) I plan to begin with support for only a few kinds of abstraction, and use hard-coded search control, and later, make the abstraction language broader and introduce decision-theoretic search control based on past experience.
Even after that is done, many issues still remain. My current approach is based on maximizing the expected value of the current game only, whereas a broader-thinking agent would also consider the utility of information gained in the current game for use in future games as well. Handling other agents better by reasoning about abstractions of their possible mental state is another crucial issue for more general and effective game-playing and planning. Finally, the ultimate challenge for planning, and AI in general, is to go beyond well-defined microworlds, and develop agents that can adapt to the complexity and ill-definedness of everyday life.
Thanks to Jon Doyle, Whitney Winston, and Carl Witty for many helpful discussions on this topic. Double thanks to Jon and Carl for comments on drafts.
Thanks also to Barney Pell for encouraging me to write this paper. Thanks to Mark Torrance for comments on the idea and on a draft of this paper.
[1] Eric B. Baum and Warren D. Smith. Best play for imperfect players and game tree search. Draft report, NEC Research Institute, May 1993. (Available for anonymous FTP from external.nj.nec.com in /pub/eric/papers/game.ps.Z.)
[2] Jon Doyle, Yoav Shoham and Michael P. Wellman. A logic of relative desire. Z. W. Ras and M. Zemankova, eds., Methodologies for Intelligent Systems, 6. Berlin: Springer-Verlag 1991, pp. 16-31.
[3] Michael P. Frank. Rational partial state-graph search. Draft report, MIT Lab for Computer Science, May 1993. (Available for anonymous FTP from medg.lcs.mit.edu in /pub/mpf/term-paper.ps.)
[4] Othar Hansson and Andrew Mayer. Probabilistic heuristic estimates. Annals of Mathematics and Artificial Intelligence, 2:209-220, 1990.
[5] Judea Pearl. Heuristics: Intelligent Search Strategies for Computer Problem Solving. Addison-Wesley series in Artificial Intelligence. Addison-Wesley, 1984.
[6] Judea Pearl. Probabilistic reasoning in intelligent systems: networks of plausible inference. Morgan Kaufmann, 1988.
[7] Stuart Russell and Eric Wefald. Principles of metareasoning. Artificial Intelligence, 49:361-395, 1991.
[8] Michael P. Wellman. Formulation of tradeoffs in planning under uncertainty. Tech report, MIT Lab for Computer Science, MIT/LCS/TR-427, August, 1988.
[9] William A. Woods. Understanding subsumption and taxonomy: a framework for progress. Tech report, Center for Research in Computing Technology, Harvard University, TR-19-90, 1990. Also appears in Principles of Semantic Networks, edited by John F. Sowa.
Footnotes
- (1)
- Work supported by an NSF graduate fellowship and by DARPA under contract F 30602-91-C-0018.
- (2)
- People also play games having complex, incomplete, and ill-defined rules, but such games are much more difficult to use as testbeds for AI research.
- (3)
- As well as, of course, the state of the rest of the world, outside the micro-world of the game.
- (4)
- For a reference on the use of description taxonomies for knowledge representation, see [8].
- (5)
- For storage efficiency in an actual implementation, abstractions would be represented using references to other abstractions, reviving the dependence on structure. But that is an implementation issue; in a conceptual, graphical representation, explicitness is important for clarity of meaning.
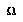 of all the possible complete histories of the world (or of the micro-world of the current game). Then let us define an abstraction
of all the possible complete histories of the world (or of the micro-world of the current game). Then let us define an abstraction 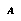 to be a description(4) of a class of world-histories. For any
to be a description(4) of a class of world-histories. For any 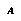 there is some subset
there is some subset 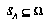 containing the world histories that satisfy the description. An abstraction will generally describe some properties of the world-history, while leaving many others unspecified. Of course, to make this definition concrete we must have some well-defined language
containing the world histories that satisfy the description. An abstraction will generally describe some properties of the world-history, while leaving many others unspecified. Of course, to make this definition concrete we must have some well-defined language 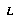 in which we express our abstractions.
in which we express our abstractions. 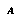
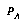
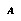
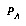
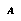
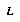 ). A proposition can include statements about the remaining time or about the present or future beliefs and intentions of the players; information that the limited concept of game position is not suited to express.
). A proposition can include statements about the remaining time or about the present or future beliefs and intentions of the players; information that the limited concept of game position is not suited to express.