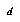 transitions of the initial state, or by using information about part of the space to jump to conclusions about the space as a whole.
transitions of the initial state, or by using information about part of the space to jump to conclusions about the space as a whole.Unfortunately, if the domain is at all interesting, we often find that the sheer size of the state-space overwhelms the computational resources available to us. But in such cases, we'd prefer not to altogether abandon the comfortable simplicity of state-space search. Instead, we compromise by searching only a part of the space.
Partial search raises two obvious issues: what part of the space do we search, and how do we use information about only a part of the space? The traditional answers to these questions have been kept as simple as possible; for example, by searching all and only those states within 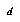 transitions of the initial state, or by using information about part of the space to jump to conclusions about the space as a whole.
transitions of the initial state, or by using information about part of the space to jump to conclusions about the space as a whole.
Recently, however, researchers have been becoming more brave. They are beginning to abandon the simplest methods, and instead look for ones that can somehow be justified as being right. To do this, they are turning to the methods of probability and decision theory. The former can tell us what to believe, the latter tells us what to do. Thus we can answer the questions of what part of the space to search, what to believe as a result, and what action, finally, to do.
Progress is being made steadily along these lines. In my opinion, the current pinnacle of this work is the recent draft paper by Eric Baum and Warren Smith of NEC Research Institute. They describe, in fairly thorough detail, a complicated but impressively well-justified set of methods for doing partial state-space search in a decision-theoretic way. The main goal of this paper is to summarize and explain these methods. A subsidiary goal, partly inspired by Baum and Smith's work, is to begin to examine how some of these methods might be generalized to guide reasoning even if some of the simplifying assumptions implicit in the classical state-space paradigm are removed.
A very common stance taken by AI programs towards possible circumstances in their domains is to think of these circumstances in terms of concrete microworld states, that is, complete assignments of values to a certain set of properties that are relevant in whatever microworld (some small piece of the world) that the program has been built to reason about. Concrete microworld states are usually just referred to in AI as world-states, or just states, but I give them the longer name to clearly identify what they are. For now, however, I will just write states.
In the stance taken by such programs, the microworld is thought of as being in a definite state at any given time; time itself is often discretized to a sequence of relevant moments, with the world changing from one state to another between moments. There is often a notion of a set of the legal or possible or consistent states that the world could ever be in; certain states are thought of as possible circumstances, while others are not. This set is referred to as the microworld's state-space.
Additionally, these programs typically have a concept of possible change, expressed in terms of primitive state transitions (or "operators" or "actions") that are imagined to transform the world from one state to another as time passes; there is imagined to be a set of allowed transitions from any given state.
The notion of a state space, together with the notion of state transitions, naturally leads to a conceptualization of domain structure in terms of a state graph, in which the nodes represent concrete microworld states, and the arcs represent the allowed state transitions.
In particular, the vast majority of the AI programs written for game-playing and puzzle-solving domains have adopted the state graph, or its specialization the state tree, as their primary conceptualization of their domain's structure. This has proved to be a natural and fruitful framework in which to develop well-defined and well-understood algorithms for reasoning in such domains. This success is no accident, since these domains are artificial ones that were defined by humans in terms of well-defined states and state-transitions in the first place. Humans make use of the state-graph conceptualization when doing analysis of these domains.
However, I will argue in §5 that, even in these state-graph-oriented domains, the state-graph conceptualization is not the only framework that humans use to support their reasoning, and that certain other models permit a greater variety of reasoning methods. I propose that the development of AI programs capable of more humanlike and general reasoning might be facilitated by research on programs that demonstrate how to use such alternative conceptual models to exhibit improved, more humanlike performance, even when applied to simple game/puzzle domains.
Given the state-graph ontology described above, it is natural to describe agents' states of knowledge about particular domain circumstances in terms of an examined partial graph, that is, a subgraph of the domain's state-graph expressing the set of nodes and arcs that the agent has examined. A node or arc is said to have been examined, or "searched," when an agent constructs a representation for it. Generally, an agent's purpose in examining part of a state-graph is to infer useful information from it. An agent might have knowledge about nodes that it has not examined; for example, it may have proven that all nodes in an entire unexamined region of the graph have a certain property. Nevertheless, we usually still consider the examined partial graph to be a special component of an agent's knowledge, because there is usually a lot of information about states that the agent can only obtain (as far as we know) by examining the corresponding part of the state-graph.
For some small game and puzzle domains (e.g., tic-tac-toe, the 8-puzzle) the state-graph is so simple so that a program can quickly examine the entire microworld state-graph. In these domains, we can obtain and process all the information we need on which to base a solution/action/decision/answer very quickly, and there is not much to say about epistemology.
More interesting are larger games, puzzles, and strategic situations, in which the state-graph may be far too large to examine in a feasible time. It may even be infinite. In such domains, the state-graph epistemology of our agents becomes an important factor in deciding how they ought to go about their reasoning. The examined partial graph cannot be the full graph, so the knowledge that will available to our agents at a time when they must make a decision will depend strongly on how the agent reasons.
I submit that the way a program answers the above two questions is a useful characteristic for categorizing AI programs whose knowledge is based on partial state-graphs. I believe that the work done by most of these programs can be naturally broken down into computation directed towards one or the other of these questions.
Many programs answer these questions incrementally, that is, they start with a small partial graph, and examine more nodes and arcs slowly, while simultaneously deriving information from the intermediate graphs, and using this information to guide the further growth of the graph. This is as opposed to creating the whole partial graph in one large atomic step and only then stopping to derive information from it.
Often the goal behind the incremental approach is to provide an anytime algorithm that can be stopped at any time and asked to immediately provide an answer based on the partial graph examined so far (such as in iterative deepening). Another reason is that if an algorithm processes states as it examines them, then it may be able to save memory by expunging most of the examined nodes and only keeping the useful information that is derived from them (such as in alpha-beta). Note that expunged nodes are still considered part of the examined partial graph, in my epistemology.
Another characteristic of most partial-state-graph-search programs is that the examined partial graph is usually connected. The connectedness is the consequence of the natural graph-examination scheme of always examining nodes that are connected to ones already examined. The connectedness property also tends to make it easier to extract useful information from the partial graph. However, one can imagine a partial graph-search scheme that examines a scattering of randomly-chosen nodes that are not inaccessibly connected to each other, or that expands the graph outwards from a small selection of unconnected search "islands."
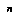 full-width minimax search.(1) Most methods are incremental to some degree; for example, alpha-beta search uses the values of some subtrees to choose which other subtrees are worth searching. A* is a single-agent example of an incremental search.
full-width minimax search.(1) Most methods are incremental to some degree; for example, alpha-beta search uses the values of some subtrees to choose which other subtrees are worth searching. A* is a single-agent example of an incremental search.
The information at the leaves is usually obtained by some heuristic function, although the heuristic may be obtained from relevant statistics about similar past nodes, rather than being hand-made by a human.
Certain of the propagation algorithms implictly assume that leaf information correctly represents a property of the entire unexplored part of the graph below that leaf. The rational approaches attempt to weaken this assumption.
A final simplifying assumption, is that many algorithms for extracting information from partial graphs assume that the graph has a restricted structure, such as that of a tree or of a DAG. The reason for assumption is that the correct algorithm is too slow or too hard to describe. Such assumptions may even be used in cases when they are known to be false; the hope is that the inaccuracies caused by the false assumptions will not degrade decision quality very much. In practice this may be true, but it makes the theoretical performance of the algorithm much harder to characterize.
Minimax assumes the correctness of some heuristic function for evaluating leaves of a tree, and it assumes perfect play by both players, and then given these assumptions, it correctly propagates those values to make a decision at the root. Minimax searches a fixed part of the space. One useful feature of minimax is that the amount of time it takes can be easily limited.
A*, on the other hand, depends on a heuristic function for search control, but makes no assumptions about the value of positions other than the solution. A* always searches until it really does find a solution, and if the heuristic isn't extremely good, that can take a long time. Thus A* might be a poor algorithm if time is important.
There have been various tweaks to these sorts of algorithms to improve their performance, such as alpha-beta search with iterative deepening. There are also many similar alternative algorithms, such as Pearl's SCOUT [3]. However, in game playing, there was, for a long time nothing that did any sort of selective search control.
Then ad-hoc methods for selective game-search, such as singular extensions, were developed. David McAllester [5] proposed a more unified, general, well-justified alternative to these methods, called conspiracy search, which roughly measured which parts of the search tree, if explored more deeply, would be most likely to have an important effect on our current situation. McAllester's method wasn't explicitly founded on probabilities or on the decision-theoretic principle of maximizing expecting utility, but it was similar in spirit; other researchers later reinterpreted McAllester's algorithm in terms of how well it approximated the decision-theoretic ideal.
Meanwhile, other researchers were looking at ways to define tree evaluation in ways that didn't make minimax's assumption of correct heuristic leaf values. The dominant method for handling uncertainty about the true value of nodes has been in terms of probability. Berliner proposed the B* algorithm [7], which worked with bounds on the probability of winning, rather than definite values. Pearl described in [3] how to use entire probability distributions over the space of game outcomes, under the assumption that distributions at different leaves are independent. However, like minimax, these distributions were over what the node value would be if we assumed perfect play by other players.
Other Hansson and Andrew Mayer [6] described a system called BPS (Bayesian problem solver) in which an ordinary evaluation function on nodes could be considered as evidence, in the Bayesian sense, of the node's true value; the probability distributions over nodes' values can then propagated through a tree like in a Bayesian belief network. An interesting characteristic of Hansson & Mayer's technique was that it used the heuristic values of interior nodes as well as those of leaf nodes; whether that might also make sense in the context of other tree-evaluation algorithms remains unclear. BPS is a well-justified way to use heuristic node values, but it says nothing about how to grow a good tree.
Another insight was that the utility of a computational action can be defined in a principled way, by estimating how that computational action (such as a leaf expansion) will improve our expected utility for our overall, external decision. I.e., computational utility should be tied to real-world utility. They pinned down the theory of this idea fairly well. Another fundamental insight was that to do this, we need nodes to have distributions that describe what our estimate of the node's value will be in the future, not Pearl's distributions over what the true value of the node is.
A third basic contribution of Russell & Wefald's work was to define the first-ever principled criteria for deciding when to stop searching: stop when the expected utility of further search becomes less than the cost of the time required to do it.
MGSS* embodied many fundamental advancements, but it had its problems. It assumed that the error distributions at nodes were normal distributions, and this required a lot of messy approximations to properly propagate these distributions up the tree. A more fundamental problem was the "single-step assumption," which defined the utility of a node expansion as just the utility of expanding the node and then immediately moving. This meant that MGSS* could only search until the tree reached what McAllester calls "conspiracy depth 1." Also, the asymptotic running time of their algorithm was a superlinear function of the size of the tree produced. Finally, after growing the tree, MGSS* just did an ordinary minimax on that tree, making the old assumption of the correctness of leaf values.
However, despite these drawbacks, Russell & Wefald demonstrated that their program performed much better than alpha-beta for a given number of nodes searched. (Note that this does not imply that it performed better for a given amount of computation time.)
Thus MGSS* paved the way for Baum and Smith's work, which contains all the advantages of Russell and Wefald's approach, and none of the above-mentioned problems.
Baum and Smith's method evaluates partial trees by backing up probability distributions from the leaves, similarly to Russell & Wefald's MGSS*. However, the Baum-Smith method gives the distributions a different semantics that facilitates the removal of Russell & Wefald's single-step assumption from the tree-growth procedure. Moreover, Baum and Smith's method doesn't require normal distributions, and so they are able to back up their distributions with no loss of information. They represent their distributions in a form that allows for extremely simple exact propagation up the tree.
Baum and Smith produce their partial trees by incremental expansion from the root state for as long as time permits. Their trees are grown by greedily expanding those leaves having the highest expected utility, as in MGSS*. However, Baum and Smith abandon Russell & Wefald's single-step assumption in their definition of the utility of leaf expansion, thus allowing the tree growth procedure to expand the tree beyond conspiracy depth one.(2) Using several mathematical and computational tricks, they approximate their ideal tree-growth procedure in an efficient algorithm.
Section 4.1 describes Baum-Smith tree evaluation, while §4.2 describes tree growth.
My description of BPIP-DFISA is broken down into several parts. First, the basis for the technique is a simple conceptualization of the problem called "the ensemble view" (§4.1.1). From this is derived a recursive strategy for node valuation called "Best Play for Imperfect Players," or BPIP (§4.1.2). However, BPIP requires a probabilistic model of future information in order to be concrete. For this, the authors provide the method called DFISA, for "Depth-First Independent Staircase Approximation" (§4.1.3). DFISA, in turn, requires an evaluation function that returns good probability distributions; Baum and Smith describe a statistics-gathering technique for generating such. (§4.1.4). Finally, information gathered at the leaves must be propagated up the tree; a few simple operations are described for doing this (§4.1.5).
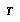 . There is presumed to be some unknown assignment
. There is presumed to be some unknown assignment 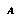 of true game-theoretic values to all the leaf nodes in
of true game-theoretic values to all the leaf nodes in 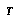 . We imagine that for each leaf node
. We imagine that for each leaf node 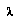 of
of 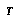 we have a probability distribution
we have a probability distribution 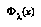 over the value that
over the value that 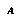 assigns to
assigns to 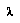 .
.
Assuming that all the 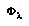 's are independent, we can derive from them a distribution over the possible assignments
's are independent, we can derive from them a distribution over the possible assignments 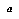 , as follows:
, as follows:
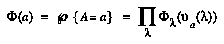 ,
,
where 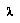 ranges over all the leaves of
ranges over all the leaves of 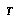 , and
, and 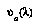 is the value that
is the value that 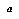 assigns to
assigns to 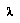 . This distribution is called the ensemble, and it allows us to define a distribution over possible values for each node
. This distribution is called the ensemble, and it allows us to define a distribution over possible values for each node 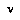 in
in 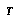 , as follows:
, as follows:
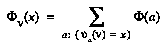 ,
,
where 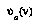 is defined as the game-theoretic (negamax) value of
is defined as the game-theoretic (negamax) value of 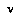 , given the leaf assignment
, given the leaf assignment 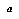 . This formula says that our probability of a node
. This formula says that our probability of a node 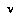 having the value
having the value 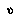 is just the sum of the probabilities of all leaf assignments in which
is just the sum of the probabilities of all leaf assignments in which 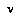 has that value.
has that value.
The problem with this ensemble method of defining node value is that it's pretty far-removed from anything approaching an actual algorithm. Summing over all possible trees is not something we can do in practice; we need a simple recursive definition of node value that we can efficiently apply. This is the role of the BPIP definition; it is equivalent to the ensemble view but expressed in terms that don't require large constructions like the ensemble.
The following definition of BPIP is a formalization of the definition that Baum & Smith informally describe.
First, some notational conventions:
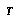 means a partial search tree.
means a partial search tree.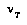 indicates the root node of
indicates the root node of 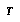 .
.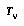 means a partial search tree that is rooted at the node
means a partial search tree that is rooted at the node 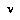 .
.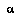 is an agent.
is an agent.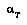 is the agent
is the agent 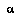 in a state of knowledge where it has direct knowledge of only those nodes that are in
in a state of knowledge where it has direct knowledge of only those nodes that are in 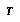 .
. 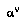 for the agent whose turn it is to move at node
for the agent whose turn it is to move at node 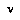 .(6)
.(6)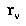 is a random variable for the desirability of the final outcome of game-play if the current players were to play from node
is a random variable for the desirability of the final outcome of game-play if the current players were to play from node 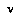 .
.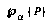 is
is 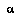 's subjective probability that the proposition
's subjective probability that the proposition 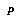 is true.
is true.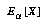 means agent
means agent 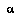 's expectation for the value of the random variable
's expectation for the value of the random variable 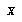 :
: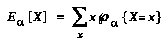 .
.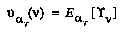 ,
,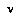 (at a time when the players will have access to a tree rooted at
(at a time when the players will have access to a tree rooted at 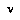 ).
).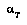 's best play
's best play 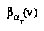 from a node
from a node 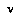 in T is that child
in T is that child 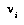 of
of 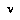 having the best subjective value
having the best subjective value 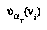 , from
, from 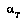 's point of view.
's point of view. 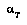 may be minimizing, maximizing, or choosing randomly (e.g., if
may be minimizing, maximizing, or choosing randomly (e.g., if 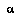 is "nature").
is "nature").
An agent 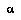 is obeying the BPIP strategy if and only if, when given only a partial tree
is obeying the BPIP strategy if and only if, when given only a partial tree 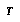 of nodes to access,
of nodes to access, 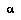 's subjective value function
's subjective value function 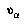 obeys the following recurrence for each interior (non-leaf) node
obeys the following recurrence for each interior (non-leaf) node 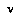 in
in 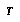 :
:
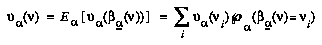
where 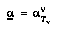 , that is, the agent
, that is, the agent 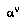 whose turn it will be at node
whose turn it will be at node 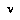 , at a time when the progress of the game has actually reached node
, at a time when the progress of the game has actually reached node 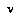 , and
, and 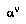 is in a knowledge state wherein he can access a different partial tree
is in a knowledge state wherein he can access a different partial tree 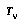 of nodes below
of nodes below 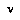 .(7)
.(7)
Additionally, if 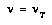 (the root of
(the root of 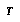 ) so that this time is now and
) so that this time is now and 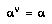 , BPIP requires
, BPIP requires 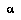 to realize that
to realize that 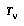 is just the current tree
is just the current tree 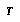 , and
, and 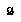 is just
is just 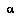 . Then EQ 5 simplifies to:
. Then EQ 5 simplifies to:
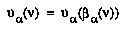 .
.
To sum up EQ 5, BPIP requires that an agent define its subjective value for interior non-root nodes to be its expectation of the value of the move that would be made from that node. EQ 6 says that the value of the root is the value of its best child.
Now, the key difference between BPIP and negamax is that BPIP doesn't require explicit maximization except at the root node; the value of an interior node is instead the sum of the children's values, weighted by the probability that the child will be chosen by 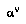 . Thus BPIP handles future actions by both players as uncertain, chance events.This is the right perspective, given the fact that, even if we know exactly how the player
. Thus BPIP handles future actions by both players as uncertain, chance events.This is the right perspective, given the fact that, even if we know exactly how the player 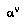 works, we do not know exactly what information will be available to him then that isn't available to us now, and thus, his choice of move is uncertain.
works, we do not know exactly what information will be available to him then that isn't available to us now, and thus, his choice of move is uncertain.
Now, BPIP is an incomplete strategy in the same way that negamax is. Like negamax, it neglects to specify how an agent gets its leaf-node values 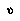 . However, unlike negamax, BPIP also depends on personal probability distributions over the
. However, unlike negamax, BPIP also depends on personal probability distributions over the 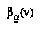 variables indicating which moves will be made at future decision points. Negamax assumes that all future decisions will be made just the way that we would make them now.
variables indicating which moves will be made at future decision points. Negamax assumes that all future decisions will be made just the way that we would make them now.
So, a BPIP agent is assumed, unlike negamax, to have some degree of knowledge about the agents involved in the game, including itself; knowledge that lets it assess how these agents will play in future situations in which different information is available. This knowledge is expressed not only by the distributions over 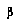 's but also through the
's but also through the 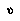 's of the leaf nodes. BPIP, unlike negamax, imposes a particular interpretation on leaf node values, namely, that they represent an expected value for the desirability of the final game outcome, given that the current players are continuing to play from a given node but with more information about the tree below that node.
's of the leaf nodes. BPIP, unlike negamax, imposes a particular interpretation on leaf node values, namely, that they represent an expected value for the desirability of the final game outcome, given that the current players are continuing to play from a given node but with more information about the tree below that node.
The authors note,
They go on to describe their chosen probabilistic model of extra information, which they call "Depth-free independent staircase approximation (DFISA)." This is described in the next section.
Recall that EQ 5 required, for each interior node, a probability distribution over the moves that a player might make at that node. A BPIP agent must provide this distribution. Can we derive this distribution solely from the values of the child nodes? If one were willing to assume that the player's future assessment of the value of the children would be the same as our current value for them, then yes, we could just declare the child that gives the best value to that player to be the one that is certain to be chosen. This is ordinary minimax. However, the point of BPIP is to move beyond this assumption, and model the fact that the valuation of a node will generally have changed by the time that node is reached in a real game. How can we model this possibility of change?
Baum and Smith's answer is to model it probabilistically. They broaden the notion of node evaluation to include not just the expected value of a node, but also a distribution over the possible future expected values for the node, that is, the values we might get for it after we do "more expansion" below it. In DFISA, the precise meaning of "more expansion" is intentionally left undefined; DFISA makes the fundamental assumption (the "depth-free approximation") that any amount of further expansion would have approximately the same effect. The idea is that the important difference is the difference between some expansion and no expansion at all. In practice, "more expansion" has a fairly definite meaning, namely, the expansion that would be done by Baum and Smith's tree-growth algorithm in a typical amount of remaining time. This is still not precise, but it is assumed by Baum and Smith to be good enough.
In any case, armed with these node-value distributions, let's look again at the problem of finding the probability that a player would make a certain move in some situation. If we knew what new values the player will have assigned to the node's children by the time the node is reached, we could predict which child the player would pick as his move. We already have distributions over the values that will be assigned to individual children, and so if we just assume independence (the "I" in DFISA), this allows us to get distributions over entire assignments of values to all the children---like in the ensemble view of §4.1.1. (Note that here we are talking about distributions over future subjective expected values, rather than distributions over true game-theoretic values, as in the ensemble view. However, the means of these two kinds of distributions are assumed to be equivalent.) Given these distributions over assignments, we can predict, in theory, the probability that a certain move will be made by summing over the assignments in which that move is the best one.
In practice this summing would be infeasible, and Baum and Smith's actual proposal for the implementation of DFISA avoids this work, and without approximation, by taking advantage of a special "staircase" (the "S" in DFISA) representation for the distributions. This will be discussed more in §4.1.5.
The leaf evaluation task is broken into two functions: a function 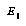 that produces an expected value for the node, and another function that returns an error distribution relative to this value. In Baum and Smith's proposal, functions for the two parts are learned separately, from different data.
that produces an expected value for the node, and another function that returns an error distribution relative to this value. In Baum and Smith's proposal, functions for the two parts are learned separately, from different data. 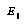 is just like an ordinary evaluation function, and can be learned in the normal way, but learning the error distributions requires a separate, special method.
is just like an ordinary evaluation function, and can be learned in the normal way, but learning the error distributions requires a separate, special method.
To produce 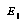 , they manually define a classification tree for chess positions, that classifies any position into a class or "bin." For each position in each game in a large library of well-played games, they categorize the position into one of these bins. Within each bin, they fit a multilinear function of positional features
, they manually define a classification tree for chess positions, that classifies any position into a class or "bin." For each position in each game in a large library of well-played games, they categorize the position into one of these bins. Within each bin, they fit a multilinear function of positional features 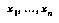 to the utility of the game's outcome. Thus, to predict the value of a new position, they simply look up the position's bin, find its feature vector, and run it through the linear function learned for that bin.
to the utility of the game's outcome. Thus, to predict the value of a new position, they simply look up the position's bin, find its feature vector, and run it through the linear function learned for that bin.
To produce the distribution-returning function, they produce another (possibly different) classification of positions into bins. They play a large number of games using  with ordinary negamax search, and for positions searched in these games, they record the change in the node's
with ordinary negamax search, and for positions searched in these games, they record the change in the node's  value obtained by deeper search (for example, depth 6). Recall that they assume the exact amount of deeper search not to be very important. They compress the set of data-points in each bin into a simpler representation of the distribution of points; the exact method for this is described in a separate paper [9].
value obtained by deeper search (for example, depth 6). Recall that they assume the exact amount of deeper search not to be very important. They compress the set of data-points in each bin into a simpler representation of the distribution of points; the exact method for this is described in a separate paper [9].
The ideal of a continuous probability density function is approximated instead by a distribution consisting of a sum of delta functions, i.e., a set of spikes. This can be thought of in mechanical terms as a set of point probability masses  at different positions
at different positions 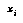 , where "position" means the value in the domain of the distribution.
, where "position" means the value in the domain of the distribution.
Second, this representation can simultaneously represent the "jumps" in a pair of staircase cumulative distribution functions that give, for each value 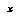 in the domain, the amount of probability mass located above (below)
in the domain, the amount of probability mass located above (below) 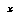 . Formally, the upper and lower CDF's
. Formally, the upper and lower CDF's 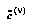 and
and 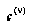 of a node
of a node 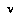 are defined by:
are defined by:
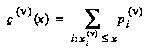
where 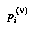 and
and 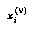 are the probability masses and abscissae (positions) of our spikes
are the probability masses and abscissae (positions) of our spikes 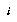 for the distribution of
for the distribution of 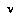 .
.
The advantage of the CDF functions is that they permit the exact computation of a distribution for a node 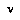 in terms of the distributions for its children
in terms of the distributions for its children 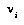 , in a way that is consistent with BPIP but skips the step in EQ 5 of computing probabilities of moves.
, in a way that is consistent with BPIP but skips the step in EQ 5 of computing probabilities of moves.
The formula for the lower CDF of a node 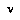 in which the an agent to move at that node is attempting to maximize his value is:
in which the an agent to move at that node is attempting to maximize his value is:
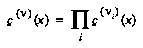 .
.
The formula for the upper CDF is similar. If we wish to have a negamax (as opposed to minimax) representation of value, we can substitute 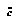 for
for 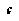 and
and 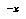 for
for 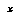 on the right side of EQ 9.
on the right side of EQ 9.
If the player at 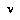 is "nature," then the formula is instead:
is "nature," then the formula is instead:
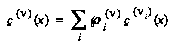 ,
,
where the 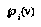 are current agent's assessments of the probabilities of the different children given the parent.
are current agent's assessments of the probabilities of the different children given the parent.
Baum and Smith say that EQ 9 can be computed quickly and exactly by something like a binary list merge on the set-of-spikes representations of the children, taking only 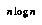 time in the number of spikes. With this technique, no information is lost as distributions are propagated up the tree.
time in the number of spikes. With this technique, no information is lost as distributions are propagated up the tree.
However, BPIP-DFISA tree evaluation takes time proportional to the number of leaves in the tree, so if the tree were deepened one leaf at a time in this way, the running time would be quadratic in the size of the final partial tree produced. Baum and Smith avoid this problem using the "Gulp trick," in which a constant fraction 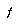 of the leaves in the tree are expanded before each re-evaluation. This ensures that the running time is dominated by the time taken by the final tree evaluation, like in traditional iterative deepening. The gulping trick is described in more detail in §4.2.1.
of the leaves in the tree are expanded before each re-evaluation. This ensures that the running time is dominated by the time taken by the final tree evaluation, like in traditional iterative deepening. The gulping trick is described in more detail in §4.2.1.
So with gulping, the goal in each stage of tree expansion is to expand that set of 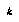 leaves whose expansion will have the highest expected utility. In order to make this feasible, Baum and Smith do two things: (1) they assume that there is an additive measure of leaf expansion importance such that the value of expanding a set of leaves is the sum of the importances of the leaves in the set. Although they disprove this assumption, they hope it will work well enough in practice. (2) They assume that expanding a leaf always makes its distribution collapse to a single point, so that expanding the most important leaves amounts to expanding those leaves whose true values we would most like to know. Baum and Smith note that making wrong assumptions such as these in tree construction is less critical than making them in tree evaluation, since they are only being used to guide tree growth and not to choose actual moves; they affect efficiency of search rather than quality of play. Also, even with these simplifications, Baum and Smith expect their search to dominate both flat search and MGSS* search.
leaves whose expansion will have the highest expected utility. In order to make this feasible, Baum and Smith do two things: (1) they assume that there is an additive measure of leaf expansion importance such that the value of expanding a set of leaves is the sum of the importances of the leaves in the set. Although they disprove this assumption, they hope it will work well enough in practice. (2) They assume that expanding a leaf always makes its distribution collapse to a single point, so that expanding the most important leaves amounts to expanding those leaves whose true values we would most like to know. Baum and Smith note that making wrong assumptions such as these in tree construction is less critical than making them in tree evaluation, since they are only being used to guide tree growth and not to choose actual moves; they affect efficiency of search rather than quality of play. Also, even with these simplifications, Baum and Smith expect their search to dominate both flat search and MGSS* search.
The measure of leaf expansion importance that they define is different from Russell & Wefald's. Recall that MGSS* assumed that the utility of expanding a leaf was equal to the utility of expanding it and then immediately moving: the "single-step assumption." The single-step assumption is bad, because it means that when the tree's conspiracy depth becomes greater than 1 (i.e., no single leaf expansion can change our choice of best move), which happens very quickly in practice, MGSS* will conclude that no expansion has utility higher than the utility of just moving without further search, so it will terminate tree-growth.
Baum and Smith instead define leaf expansion importance with a measure they call "Expected Step Size," or ESS. The ESS of a leaf-expansion is essentially the absolute amount that we expect it will change our expected utility for all possible future expansion. In other words, if we think that expanding a certain leaf will clarify, one way or the other, the value of future expansion, then that leaf is a good one to expand. If it lowers our utility for future expansion, it prevents us from wasting time doing more expansion, and if it raises our utility for expansion, it prevents us from quitting and making a move too early. Baum and Smith's quitting criteria are discussed in §4.2.5.
Interestingly, ESS can be thought of as an instance of a more general principle of limited rationality, which is that learning more about the value of actions is a very valuable action in itself. When you're starting to do a round of expansion, first consider what you will do afterwards. There are two possible actions: you can either move right away after this round, or you can continue doing more expansion. You have some current utility for each of these actions, and some current best action. However, these utilities are uncertain. You might have a distribution over how your utility for each of these actions will change after this round of expansion. If these distributions overlap, then you'd like for your next round of expansion to tighten up those distributions, so as to tell you for certain whether or not to go on and do another round.
Baum and Smith don't have a distribution over the utility of continuing to compute, or a model of how much certain leaf expansions will tighten it. Instead, they estimate how much a particular leaf expansion will perturb the mean of the distribution; the assumption being that large perturbations correspond large tightenings of the distribution.
ESS can be computed using the concept of "influence functions," which express the amount that some quantity at the root node will change if some quantity at one root changes while other roots remain fixed. These will be described in §4.2.4.
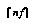 most important leaves, where
most important leaves, where 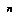 is the current number of leaves and
is the current number of leaves and 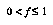 is a constant fraction determined empirically. Thus the cost of re-evaluating the tree after each growth step is amatorized over a large number of new nodes produced, and the total cost of all steps is dominated by the time for the final tree evaluation.
is a constant fraction determined empirically. Thus the cost of re-evaluating the tree after each growth step is amatorized over a large number of new nodes produced, and the total cost of all steps is dominated by the time for the final tree evaluation.
Baum and Smith describe the efficiency of gulping in terms of a constant slowdown factor 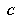 which describes, given
which describes, given 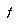 and the average branching factor
and the average branching factor 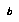 , how much time the tree growth (with gulping) takes compared to the time to evaluate the final tree produced---assuming that the average branching factor is larger than 1. The slowdown factor for chess is computed to be 2.2 for
, how much time the tree growth (with gulping) takes compared to the time to evaluate the final tree produced---assuming that the average branching factor is larger than 1. The slowdown factor for chess is computed to be 2.2 for 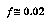 .
.
Now, the gulp trick is an approximation; more ideal would be to re-evaluate the tree after each node expansion. In some circumstances, gulping might grow much worse trees than the ideal. To illustrate, imagine a chess position in which there is a single, long, clearly-forced sequence of moves following that position, where the ideal would be to trace down that forced sequence to see how it comes out, before examining other possibilities. With gulping, however, we would expand other nodes in parallel with each step down the forced path; a larger and larger set of them each time. So we would not get very far down the forced path.
Still, we expect to get farther down the forced path than flat alpha-beta would. And we don't usually expect there to be only one forced line like this; in general we expect that the number of reasonable variations increases exponentially with tree size; if 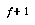 is tailored to fit this exponent, then gulping should usually do well. We cannot make
is tailored to fit this exponent, then gulping should usually do well. We cannot make 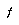 too small, however, because then the slowdown factor will increase.
too small, however, because then the slowdown factor will increase.
In summary, gulping seems like it ought to do fairly well for chess. To handle a more general range of problems, we might want the tree-growth algorithm to try to adapt the value of 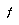 to fit the needs of the problem at hand, but Baum and Smith don't discuss this.
to fit the needs of the problem at hand, but Baum and Smith don't discuss this.
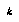 of the leaves of the current tree before proceeding, the problem within that policy is how to find the set of
of the leaves of the current tree before proceeding, the problem within that policy is how to find the set of 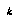 leaves whose expansion would give us the highest expected utility. Baum and Smith describe a solution that gives the ideal decision-theoretic way to derive the utility of expanding any subset of leaves, given the CDF's for the children of the root, and the assumption mentioned earlier about distributions collapsing to a point. The definition essentially sums over all possible moves that might be found to be better than our current best move, and over the amounts that it might be better, if that set of leaves were expanded. (This is similar to one of Russell & Wefald's definitions.) However, to apply this definition to the problem of choosing the right subset of leaves, it seems necessary to apply it to all the subsets, which is clearly infeasible.
leaves whose expansion would give us the highest expected utility. Baum and Smith describe a solution that gives the ideal decision-theoretic way to derive the utility of expanding any subset of leaves, given the CDF's for the children of the root, and the assumption mentioned earlier about distributions collapsing to a point. The definition essentially sums over all possible moves that might be found to be better than our current best move, and over the amounts that it might be better, if that set of leaves were expanded. (This is similar to one of Russell & Wefald's definitions.) However, to apply this definition to the problem of choosing the right subset of leaves, it seems necessary to apply it to all the subsets, which is clearly infeasible.So instead, Baum and Smith simplify the problem by assuming that the utility of expanding any set of leaves is just the sum of a measure, called the leaf expansion importance, that is evaluated for each leaf in the set. They in fact prove, with a counter-example, that no such measure can exist. However, they proceed in the hope that it will "often be approximately true," as with their other simplifying assumptions.
One possible importance measure, which Baum and Smith call "Single-Leaf Expansion Utility" (SLEU) would incorporate Russell & Wefald's single-step assumption. However, Baum and Smith dismiss this measure because of the limitation to conspiracy-depth-1 trees, and for other reasons which I won't go into here.
Instead, the authors do the following: they evaluate the above-mentioned true utility of expansion for the set of all leaves, and consider this to be the expected utility of all future expansion (EUAFE). In other words, it would be the expected utility of knowing the true values of all the leaves in the tree. To make sense of this, think of it as the expected cost of proceeding with our current guesses for the leaf values instead---in other words, how likely is it that our current guesses are wrong.
This EUAFE measure is then used to define the ESS leaf-importance measure, in a way that implicitly seems to identify the EUAFE with the expected utility  of the action "continue to expand the tree" (as opposed to "stop and make a move now"), although Baum and Smith do not themselves make this identification. Since, in continuing to expand the tree, we will probably not actually expand all the leaves, this interpretation of EUAFE is not exactly correct.
of the action "continue to expand the tree" (as opposed to "stop and make a move now"), although Baum and Smith do not themselves make this identification. Since, in continuing to expand the tree, we will probably not actually expand all the leaves, this interpretation of EUAFE is not exactly correct.
(However, Baum and Smith do not actually characterize ESS in terms of U_continue.)
The "Expected step size," or ESS, of a leaf is defined to be the expected absolute value of the change in [???] that would be caused by expanding that leaf (reducing its distribution to a point) while keeping other leaves' distributions the same. As I described in the introduction to §4.2, this can be seen as an approximate measure of the expected improvement in the quality of our decision about whether to continue doing more expansion after the current round of it is over.(8) Unfortunately, Baum and Smith do attempt to justify ESS in these terms, and instead put forth a number of less satisfying arguments of why ESS is a good measure. They do, however, provide an approximation theorem that describes ESS in utilitarian terms [say more].
[I would subjectively judge ESS to be the weakest link in Baum and Smith's technique, and the part most in need of empirical justification. (change mind?)]
One nice thing about the ESS measure is that it can be computed quickly from a node's influence function. An influence function describes how changes in the node will affect the root's value. The influence function can, in turn, be computed in time only linear in the number of nodes in the tree. Baum and Smith provide fairly detailed pseudo-code for the computation of ESS and influence functions in an appendix, so I will not attempt to reinvent their algorithm here.
Thus, Baum and Smith's influence-function computation works by traversing the tree downward from the root, accumulating factors into these constants on the way down the tree. The total work is proportional to the number of nodes.
However, this way of handling time is not very theoretically satisfying. There's very little to be said about exactly why, and when, and how well this technique will really approximate maximization of our probability that we will win the game, or find the solution on time. What will happen if the rules of the game depend on time in a more complicated way than in chess? Even for chess, this treatment of time is weak: for example, suppose the opponent is running low on time and we are not. To maximize the probability of winning, we ought to try to steer play into complicated situations, where careful thinking is required in order to avoid making a blunder, in the hope that the opponent, in his rush, will make a mistake. Treating time as external to the domain, and only using it to cap computation time, doesn't address this kind of reasoning at all. I will discuss the issue of time some more in §5.
In doing away with some of the assumptions of traditional minimax, Baum and Smith have to make quite a few new, untested simplifying assumptions and approximations. Many of these are fairly well-justified by Baum and Smith's theoretical arguments, and it seems that the problems aren't too serious, but it remains to be seen how well they will work in practice. A list of some of the assumptions and approximations:
I heartily agree with this sentiment, and I would like to propose that it applies not just to game-playing but to the similar search methods often used in puzzle- and problem-solving domains. I also propose that in questioning the current approach, we ought to try to reveal all of its hidden assumptions (which I attempted to enumerate in §2), and determine which are most necessary for future progress, and which would be beneficial to try working without. Sections §5.1 and §5.2 reexamine a few of these assumptions and suggest how they might be relaxed. Sections §5.3 and §5.4 examine some unrelated methodological issues.
So why don't people include these properties, which are, after all, relevant to the game, in the concept of a game state? The reason is that games researchers realize that including these properties would ruin the performance of their game-search algorithms. Why? Because all of a sudden there would be many more states than before, many of them differing only in these two properties. It multiplies the size of the problem a thousandfold.
But since these properties are important to they game, how can game-programs play well while ignoring them? After all, games researchers don't ignore other properties, such as the positions of pieces.
The answer is that the games researchers have encoded, in their definition of state, domain-specific knowledge to the effect that these properties usually aren't very important to things we care about, such as the expected utility of a state. Usually, in a game like chess, the utility of a board position is the same no matter how you got there, or exactly what time it is. In other words, the program designers have built in an abstract notion of state, not a concrete one at all, because they realize that the abstraction is useful; it provides a good approximation to the more computation-intensive ideal of considering the position history and game time.
This raises a number of very interesting questions:
Most of these questions are still unanswered, and even still poorly-defined. At best they only hint at a future direction. However, I think I have begun to make some progress in answering some of them in my thesis work.
One preliminary conclusion is that transplanting rational techniques from complete state-space search to abstract state-space search is probably not so hard after all. It is made easier by the observation above that existing game-state-spaces are really abstract spaces already, and thinking of them in those terms makes it easier to see how the current methods might make sense with other kinds of abstraction as well.
One might think that it would be easier to first try transplanting simple techniques like minimax before attempting to generalize all of Baum-Smith search to a world of abstract states. On the contrary, I think that a decision-theoretic approach is vital for properly handling all of the uncertainties and all of the questions of usefulness that are involved in any sort of abstract reasoning. I think that some of the previous attempts in AI to do related things such as "chunking" and "reasoning by analogy" have been relatively unsuccessful because they did not take a proper decision-theoretic stance---of plausible inference and cost-effective action---towards the selection and use of the abstract generalizations that they were making.
In my ongoing research, I plan to soon begin illustrating the use of simple rational abstraction in the game of spider solitaire, which offers some good opportunities for rational abstraction and search-control to show themselves off. Spider also serves as an example of a very large single-agent decision-analysis problem. Hopefully I will also be able to generalize rational abstraction methods to be of some use in other large decision problems as well.
This raises an issue of methodology: as computer game-playing/problem-solving researchers, should we focus a lot of our effort on encoding lots of domain-specific knowledge into programs that introduce new, supposedly general techniques?
I would argue that the answer is no. Groveling over an evaluation function might be the wrong place to focus attention; we should be looking at methods to reduce the amount of human effort required to tailor the evaluation function, and make the computer do more of the work. Besides saving time, we might learn general machine-learning techniques, which we could apply to other areas.
For example, in Appendix A, I describe a method for constructing good classification spaces automatically from a set of features, by explicitly measuring how well a classification space performs at predicting the data of interest (here, a position's value). We would do well, I think, to use such automated methods when possible, so as to minimize the amount of time we spend writing hand-tailored domain-specific code.
Also, as Matt Ginsberg has argued [10], there are generally domain-independent reasons why domain-specific tricks work. If we expend a little extra effort to find those more-general forms for our computational tricks and techniques, we stand the chance of gaining great benefits when we learn how we, and our agents the computers, can apply that knowledge in other areas.
Many people like to work on well-established AI problems, so that the relevance of their work can be easily demonstrated by comparing their new program's performance with that of well-established, earlier programs. However, I feel that comparison with existing programs in traditional domains can be extremely misleading. These programs usually win not because they have better general intelligence, but because they're more narrowly focused and specialized to that one small domain.
This is especially true for chess. I think that, in particular, the computer chess community has gone much too far in the direction of domain-specific hacking, for chess competitiveness to be a good measure of the worthiness of, say, a new general theory of search. It's possible that someday, smart AI programs will beat the brute-force chess engines, but the chess hackers have too much of a head start for chess to be a good place, in my opinion, for an AI researcher to start.
So, if we abandon comparison against programs in well-established narrow domains as a good basis for evaluating AI techniques, how can we evaluate our methods? One solution, proposed by Barney Pell in [8], is to try to establish a new, broader competitive problem domain; one for which even a program that was very domain-specific would still need lots of general reasoning mechanisms.
Another idea, which is easier because it can be implemented on the individual level, is as follows:
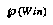 that we would win if we were in that game position. Or, if it's a game with several possible outcomes
that we would win if we were in that game position. Or, if it's a game with several possible outcomes 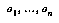 , we may want a probability distribution
, we may want a probability distribution 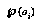 over these outcomes. Or, for control of search, we may want, for each
over these outcomes. Or, for control of search, we may want, for each 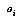 , some approximate representation of a continuous distribution over the amount that our
, some approximate representation of a continuous distribution over the amount that our 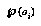 for the position will change after some more computation. In any of these cases, the problem is the same: how do we do a quick, yet high-quality assessment of these probabilities?
for the position will change after some more computation. In any of these cases, the problem is the same: how do we do a quick, yet high-quality assessment of these probabilities?
One good answer is to get these probabilities by collecting statistics. Unfortunately, in real games there are far too many positions to feasibly collect statistics for each of them individually. The standard solution to this problem is to collect statistics for whole classes of positions at once, without remembering the statistics for the individual positions within a class. The classification space for positions is often defined as the cross-product of a number of feature spaces 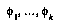 , each of which is the range of a feature
, each of which is the range of a feature 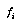 , which is some easily-computed function of game positions (see Figure 1, "Classification Spaces," on page 27). We generally try to choose a classification space that we think will provide a lot of information about the variable we're interested in (the game outcome, or our future probability assessment).
, which is some easily-computed function of game positions (see Figure 1, "Classification Spaces," on page 27). We generally try to choose a classification space that we think will provide a lot of information about the variable we're interested in (the game outcome, or our future probability assessment).
Once we've defined our classification space, or set of bins, we can begin gathering statistics from our data. Each data point is assumed to be in the form of a game position 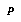 , together with the value of the variable
, together with the value of the variable 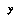 we are interested in. We classify
we are interested in. We classify 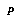 , look up a data storage bin for its class, and add
, look up a data storage bin for its class, and add 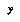 to the data stored in that bin. We might also associate
to the data stored in that bin. We might also associate 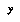 with some additional information about
with some additional information about 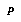 that know relates to
that know relates to 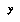 in a certain special way; for example, if
in a certain special way; for example, if 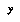 is numeric, we might expect its value to be correlated with the values of certain numeric features
is numeric, we might expect its value to be correlated with the values of certain numeric features 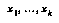 ; these features would then be left out of the feature set used to define the classification space, and instead their values would be stored along with the value of
; these features would then be left out of the feature set used to define the classification space, and instead their values would be stored along with the value of 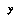 . (A la Baum and Smith.)
. (A la Baum and Smith.)
Then, for each bin, we form a model of the data in that bin, in the form of a probability distribution over 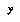 (or, in the case where additional information is stored in the bin, a function from
(or, in the case where additional information is stored in the bin, a function from 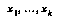 to distributions over
to distributions over 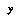 ). We might get the distribution by choosing the maximum-likelihood distribution given the data, out of some simple space of approximate representations of distributions.
). We might get the distribution by choosing the maximum-likelihood distribution given the data, out of some simple space of approximate representations of distributions.
So then we're done; when we see a game position, we simply look up its bin and use the stored probability distribution as our quick first assessment of our belief about which outcome will actually occur.
Unfortunately, we often find that it's hard to come up with one simple feature that does at well at predicting the outcome. Even combinations of 2 or 3 simple features might not be
enough. We generally find that we need a lot of features in order for the statistics to discriminate the different outcomes well. However, this leads to another problem: the more features we have, the larger the classification space becomes (exponentially), and so a huge amount of data is required in order to get a statistically significant sample in each class.
FIGURE 1. Classification Spaces
The point of this paper is to briefly describe one possible solution to this problem. This method is not original with me, but it's been a long time since I worked on this and I don't remember the references; I'm in the process of tracking them down.
For example, we could form a classification space for each combination of 1, 2, or 3 different features. Each data point can be classified within each space, so we only need to collect enough data to get a good sample in each bin of the largest such space.
But when it comes time to use the results, how do we combine the probability distributions produced by a position's classification in all the different spaces? We don't want to just add them together, because some of them will be much better predictors of the outcome than others; we want them to contribute to the answer proportionately. Is there any principled way to weight the distributions?
Well, here is one possibility. Each classification space, with probability distributions in all of its bins, can be thought of as a probabilistic model of the data, i.e., as a hypothesis that a position's outcome is determined by selecting a value from a its class's distribution. Thought of in this way, we can say that each classification space, each hypothesis, has some probability of being the "correct" one. If we could only compute this probability, it would make sense to use that as the space's weight. (Assuming that all these hypotheses are mutually exclusive---the damage of assuming this in practice is hoped to be small.)
We can compute model probabilities using Bayes' rule. Since these are probabilistic models, it's trivial to compute the likelihood of the data given the model. So the problem is reduced to one of finding sensible priors for all the models. This is not too critical since, with a good statistical sample in all of a model's bins, the differences in the data-likelihood between the different spaces ought to be the deciding factor.
In any case, the prior for a classification-space model is just the product of the priors for the distributions in each of its bins, since the classification-space can be thought of as a conjunctive hypothesis of the form "in this bin, the distribution is this; and in this other bin, it's this; etc..."
How we compute a prior for the distributions in the bins depends on how we represent the distributions, and whether we have additional stored features (Baum and Smith's 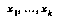 ) complicating our model. However, one answer in the simple case is that the prior ought to be just
) complicating our model. However, one answer in the simple case is that the prior ought to be just 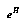 , where
, where 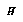 is the entropy of the probability distribution in the bin; a high-entropy distribution carries less information and so should be a priori more probable.
is the entropy of the probability distribution in the bin; a high-entropy distribution carries less information and so should be a priori more probable.
In God, one player is the "god," and makes up a rule determining what stacks of cards are "allowed." For example, the rule might say that a stack is allowed if and only if the top card has a different suit and than either of the next two cards. The other player starts with all the cards, and he attempts to play them one at a time on a growing stack; after each attempt the god says "yes," or "no;" if "no," the player must take back the card and try again. The player's goal is to get rid of the cards as quickly as possible. Assuming a greedy strategy, his goal on each play is to play the card that forms a stack having the highest probability of being allowed, based on the answers received so far. (Other rules prevent the God from making the rule too restrictive or complicated; I won't go into those here.)
One thing to note is that the data is very scant; in a well-played game the player receives only a few bits per card. Thus my collaborator Mark Torrance and I required a technique that used the data very efficiently. We defined about ten features of card stacks, for example, whether the top two cards were the same suit. We then formed classification spaces for every combination of one or two of these features, and derived predictions from past data as described above. The technique proved very effective in generating good predictions, our player was the best out of about a half-dozen God-playing programs written for a class.
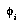 and
and 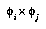 , if the outcome is totally independent of
, if the outcome is totally independent of 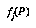 given
given 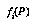 , because
, because 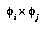 will then represent the same hypothesis as
will then represent the same hypothesis as 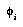 . Thus
. Thus 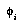 's contribution to the total distribution will be unfairly magnified. This particular case should not be a serious problem, since
's contribution to the total distribution will be unfairly magnified. This particular case should not be a serious problem, since 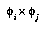 will have a negligible probability compared to
will have a negligible probability compared to 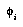 , as a result of it being a much larger space and so having a much smaller prior. But if two identical features are included by accident, their contribution will be counted twice; and any two features that are not independent will degrade the prediction quality, to a degree that is still unclear.
, as a result of it being a much larger space and so having a much smaller prior. But if two identical features are included by accident, their contribution will be counted twice; and any two features that are not independent will degrade the prediction quality, to a degree that is still unclear.Another problem is that we are considering only models that contain maximum-likelihood distributions for the data. What if we also considered, in each space, a continuum of nearby models that contained distributions that were slightly different? Might that yield different weights for our classification spaces?
To avoid this problem, we need to make sure that our distributions are not just "most likely" distributions but rather express the sum of all possible distributions, weighted by their probability given the data. If we do this, then we can be sure that when we calculate the probability of a classification space, we are truly calculating the probability of just the hypothesis that it's the right space, not the hypothesis that it's the right space and that the distribution in each node is such-and-such particular distribution.(9)
If the variable 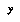 has a small, discrete range (e.g.,
has a small, discrete range (e.g., 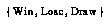 ), and we accept a normal flat prior over the space of possible distributions over
), and we accept a normal flat prior over the space of possible distributions over 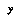 , then there is no problem; a standard formula(10) for the exact distribution is given by:
, then there is no problem; a standard formula(10) for the exact distribution is given by:
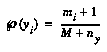
where 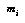 is the number of data points where
is the number of data points where 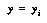 ,
, 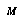 is the total number of data points
is the total number of data points 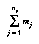 , and
, and 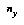 is the number of possible values of the variable
is the number of possible values of the variable 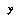 . This formula works well even on small amounts of data. Note that when there is no data, we get a flat distribution; this is the correct weighted sum of all possible distributions if all are equally likely. If there are two outcomes
. This formula works well even on small amounts of data. Note that when there is no data, we get a flat distribution; this is the correct weighted sum of all possible distributions if all are equally likely. If there are two outcomes  and the data has 1 win and no losses in the bin, when we get
and the data has 1 win and no losses in the bin, when we get 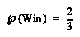 .
.
However, if the range of 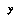 is continuous (or just too large to store all the
is continuous (or just too large to store all the 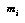 's), as is the case if
's), as is the case if 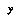 represents a future probability assessment, then we cannot use EQ 11 directly. In any case, we probably don't want our prior over distributions over such a large space to be flat; smooth, simple distributions seem more likely a priori than complex, jagged ones with high spatial frequencies.
represents a future probability assessment, then we cannot use EQ 11 directly. In any case, we probably don't want our prior over distributions over such a large space to be flat; smooth, simple distributions seem more likely a priori than complex, jagged ones with high spatial frequencies.
One simple method that ignores high spatial frequencies but still allows multimodal distributions is to discretize 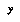 into evenly-spaced sections, and use EQ 11 on those. However, this loses the distinction between a needle-sharp peak and a slightly smoother one that's still all in one discrete section.
into evenly-spaced sections, and use EQ 11 on those. However, this loses the distinction between a needle-sharp peak and a slightly smoother one that's still all in one discrete section.
I have thought of a few more complex ways to try to deal with this issue, but I'll save them until they're better developed.
In the previous proposal, we weighted a classification space's prediction of a game-position's outcome by the probability that the entire classification space was the "right" model of the data. However, each game-position lies in only one bin in each classification space. So perhaps, the probability of that individual bin, rather than that of the entire space, would be the more appropriate quantity for weighting the bin's prediction.
However, this raises a couple of new problems. It complicates the question of whether two alternative hypotheses are independent. Also, it complicates the comparison of the probability of the two hypotheses, since in general they will have been based on different data.
Further work remains to be done on this alternative.